Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: ΔOAB cân tại O
mà OH là đường trung tuyến
nên OH\(\perp\)AB
Ta có: ΔOHA vuông tại H
=>\(HA^2+HO^2=OA^2\)
=>\(HA^2=5^2-3^2=16\)
=>\(HA=\sqrt{16}=4\left(cm\right)\)
H là trung điểm của AB
=>AB=2*AH=8(cm)

a: Ta có: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>\(HA=HB=\dfrac{AB}{2}=2,4\left(cm\right)\)
Ta có: ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(OH^2=3^2-2,4^2=3,24\)
=>\(OH=\sqrt{3,24}=1,8\left(cm\right)\)
OH+HC=OC
=>HC=OC-OH=5-1,8=3,2(cm)
b: Ta có: ΔAHC vuông tại H
=>\(AH^2+HC^2=AC^2\)
=>\(AC^2=2,4^2+3,2^2=16\)
=>\(AC=\sqrt{16}=4\left(cm\right)\)
Xét ΔAOC có \(AO^2+AC^2=OC^2\)
nên ΔAOC vuông tại A
=>CA\(\perp\)OA tại A
=>CA là tiếp tuyến của (O)
b: Xét ΔCAB có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAB cân tại C
=>CA=CB
Xét ΔOAC và ΔOBC có
OA=OB
AC=BC
OC chung
Do đó: ΔOAC=ΔOBC
=>\(\widehat{OAC}=\widehat{OBC}=90^0\)
=>CB là tiếp tuyến của (O)
Xét (O) có
EA,ED là các tiếp tuyến
Do đó: EA=ED
Xét (O) có
FD,FB là các tiếp tuyến
Do đó: FD=FB
Chu vi tam giác CEF là:
\(CE+EF+CF\)
=CE+ED+DF+CF
=CE+EA+CF+FB
=CA+CB
=2CA
=8(cm)

Lời giải:
Tam giác $OAB$ cân tại $O$ (do $OA=OB=R$) nên đường trung tuyến $OH$ đồng thời là đường cao.
$\Rightarrow OH\perp AB$
$AH=\frac{1}{2}AB=8$ (cm)
Áp dụng định lý Pitago cho tam giác vuông $HAO$:
$R=AO=\sqrt{OH^2+AH^2}=\sqrt{6^2+8^2}=10$ (cm)
Đáp án D.

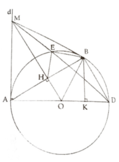
a, Tính được AH = 5 . Từ đó suy ra AB= 2 5 và OM=4,5cm
b, Với ∆MAB cân tại MH là trung tuyến vừa là đường cao;
Ta có ∆MAO = ∆MBO => MBOB => MB là tiếp tuyến của (O)
c, Dễ thấy M A 2 = M H . M O (Theo hệ thức lượng trong tam giác vuông)
Chứng minh được: ∆MBE:∆MBD
=> M B 2 = M E . M D = M A 2
=> MH.MO = ME.MD
=> ∆EHM:∆ODM (c.g.c)
=> E H M ^ = O D M ^
d, Kẻ BK ⊥ AD
Ta có: S H O A = 1 2 S A B D = 1 4 B K . A D
Vì BK ≤ 3 => S H O A lớn nhất khi B là điểm chính giữa cung AD khi đó AM = OA = 3
Sửa đề: OH=3cm