
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a,
\(C=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{19}\\ C>0+0+0+...+0=0\left(1\right)\)
\(C=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{19}\)
Ta có:
\(\dfrac{1}{11}< \dfrac{1}{10}\\ \dfrac{1}{12}< \dfrac{1}{10}\\ \dfrac{1}{13}< \dfrac{1}{10}\\ ...\\ \dfrac{1}{19}< \dfrac{1}{10}\)
\(\Rightarrow C< \dfrac{1}{10}+\dfrac{1}{10}+\dfrac{1}{10}+...+\dfrac{1}{10}\left(9\text{ phân số }\dfrac{1}{10}\right)\\ C< 9\cdot\dfrac{1}{10}\\ C< \dfrac{9}{10}< 1\left(2\right)\)
Từ (1) và (2) ta có:
\(0< C< 1\)
Rõ ràng \(0\) và \(1\) là hai số nguyên liên tiếp nên \(C\) không phải là số nguyên
Vậy \(C\) không phải là số nguyên (đpcm)
b,
\(D=2\left[\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{n\left(n+2\right)}\right]\\ D=\dfrac{2}{3}+\dfrac{2}{15}+\dfrac{2}{35}+...+\dfrac{2}{n\left(n+2\right)}\\ D>0+0+0+...+0=0\left(1\right)\)
Ta có:
\(D=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{n\cdot\left(n+2\right)}\\ D=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{n}-\dfrac{1}{n+2}\\ D=\dfrac{1}{1}-\dfrac{1}{n+2}\\ D=1-\dfrac{1}{n+2}< 1\left(\text{Vì }n>0\right)\left(2\right)\)
Từ (1) và (2) ta có:
\(0< D< 1\)
Rõ ràng \(0\) và \(1\) là hai số nguyên liên tiếp nên \(D\) không phải là số nguyên
Vậy \(D\) không phải là số nguyên (đpcm)
c,
\(E=\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\\ E=\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\\ E=\dfrac{2}{6}+\dfrac{2}{7}+\dfrac{2}{8}+\dfrac{2}{9}+\dfrac{2}{10}+\dfrac{2}{11}\)
Ta có:
\(\dfrac{2}{6}>\dfrac{2}{12}\\ \dfrac{2}{7}>\dfrac{2}{12}\\ \dfrac{2}{8}>\dfrac{2}{12}\\ ...\\ \dfrac{2}{11}>\dfrac{2}{12}\)
\(\Rightarrow E>\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}\\ E>6\cdot\dfrac{2}{12}\\ E>\dfrac{12}{12}=1\left(1\right)\)
Mặt khác ta có:
\(\dfrac{2}{6}>\dfrac{2}{7}\\ \dfrac{2}{6}>\dfrac{2}{8}\\ \dfrac{2}{6}>\dfrac{2}{9}\\ ...\\ \dfrac{2}{6}>\dfrac{2}{11}\)
\(\Rightarrow E< \dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}\\ E< 6\cdot\dfrac{2}{6}\\ E< 2\left(2\right)\)
Từ (1) và (2) ta có:
\(1< E< 2\)
Rõ ràng \(1\) và \(2\) là hai số nguyên liên tiếp nên \(E\) không phải là số nguyên
Vậy \(E\) không phải là số nguyên (đpcm)
c) \(E=\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\)
\(=\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\)
\(=2\left(\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}+\dfrac{1}{11}\right)\)
Ta có: \(\dfrac{1}{6}>\dfrac{1}{7}>\dfrac{1}{8}>\dfrac{1}{9}>\dfrac{1}{10}>\dfrac{1}{11}\)
\(\Rightarrow E>2\left(\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}\right)=2\left(\dfrac{1}{11}.6\right)=2\cdot\dfrac{6}{11}=\dfrac{12}{11}>1\) (1)
\(E< 2\left(\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}\right)=2\left(\dfrac{1}{6}.6\right)=2.1=2\) (2)
Từ (1) và (2) suy ra 1 < E < 2 suy ra E không phải là số nguyên

Bài 6:
a) \(\widehat{MAP}=\widehat{NAQ}\) (hai góc đối đỉnh)
Mà \(\widehat{MAP}=33^o\)
Vậy \(\widehat{NAQ}=33^o\).
b) Ta có: \(\widehat{MAP}+\widehat{MAQ}=180^o\) (hai góc kề bù)
Mà \(\widehat{MAP}=33^o\)
Nên \(\widehat{MAQ}=180^o-\widehat{MAP}=180^o-33^o=147^o\)
Vậy \(\widehat{MAQ}=147^o.\)
c) Các cặp góc đối đỉnh:
\(\widehat{MAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAP}\) và \(\widehat{MAQ}\).
d) Các cặp góc bù nhau:
\(\widehat{MAP}\) và \(\widehat{NAP}\)
\(\widehat{NAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAQ}\) và \(\widehat{MAQ}\)
\(\widehat{MAQ}\) và \(\widehat{MAP}\).

Gọi số cuốn sách tham khảo môn Toán lớp 6, lớp 7 và lớp 8 mà thư viện đó mua lần lượt là x, y, z (x, y, z \( \in \)\(\mathbb{N}\))
Vì tổng cộng là 121 cuốn nên ta có \(x + y + z = 121\)
Vì số tiền dùng để mua mỗi loại sách đó là như nhau nên số cuốn sách và giá tiền một cuốn sách tương ứng là 2 đại lượng tỉ lệ nghịch.
Theo tính chất hai đại lượng tỉ lệ nghịch, ta có:
\(40.x=45.y=50.z \Rightarrow \dfrac{x}{{\dfrac{1}{{40}}}} = \dfrac{y}{{\dfrac{1}{{45}}}} = \dfrac{z}{{\dfrac{1}{{50}}}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{{\dfrac{1}{{40}}}} = \dfrac{y}{{\dfrac{1}{{45}}}} = \dfrac{z}{{\dfrac{1}{{50}}}}= \dfrac{{x + y + z}}{{\dfrac{1}{{40}} + \dfrac{1}{{45}} + \dfrac{1}{{50}}}} = \dfrac{{121}}{{\dfrac{{121}}{{1800}}}} = 121.\dfrac{{1800}}{{121}} = 1800\\ \Rightarrow x = 1800.\dfrac{1}{{40}} = 45\\y = 1800.\dfrac{1}{{45}} = 40\\z = 1800.\dfrac{1}{{50}} = 36\)
Vậy số sách tham khảo môn Toán lớp 6, lớp 7 và lớp 8 mà thư viện đó mua lần lượt là 45 quyển, 40 quyển và 36 quyển.

Bài 1. Cho tam giác ABC, có góc A = 90º, d là đường thẳng qua C và vuông góc với BC; tia phân giác của góc B cắt AC ở D và cắt d ở E. Kẻ CH vuông góc với DE, H thuộc DE. Chứng minh CH là tia phân giác của góc DCE?
Bài 2: Cho tam giác ABC, góc B > góc C, AD là tia phân giác
a) Chứng minh góc ADC - ADB = góc B - C
b) Phân giác góc ngoài tại A của tam giác ABC cắt BC ở E. Chứng minh góc AEB = 1/2 (B -C)
Bài 3: Cho tam giác ABC, gọi D, E lần lượt là trung điểm của AC, AB. Trên tia đối của tia DB lấy M sao cho DM = DB; trên tia đối của tia EC lấy N sao cho EN = EC. Chứng minh A là trung điểm của MN?
Bài 4: Cho tam giác ABC có góc A = 50°. Vẽ đoạn thẳng AI vuông góc và bằng AB (I và C khác phía với AB). Vẽ đoạn thẳng AK vuong góc và bằng AC (K và B khác phía với AC). Chứng minh:
a) IC = BK
b) IC vuông góc BK
Bài 5: Cho tam giác ABC có góc A = 100°, M là trung điểm của BC, trên tia đối của MA lấy K sao cho MK = MA
a) Tính số đo góc ABK?
b) Ở phía ngoài tam giác ABC, vẽ AD vuông góc và bằng AB, AE vuông góc và bằng AC. Chứng minh hai tam giác ABK và DAE bằng nhau
c) Chứng minh MA vuông góc DE
Bài 6: Cho tam giác ABC có tia phân giác của góc ABC cắt cạnh AC ở D, tia phân giác của góc ACB cắt cạnh AB ở E. Biết BE + CD = BC. Tính số đo góc BAC?
Bài 7: Cho tam giác ABC có góc B = 2C. Tia phân giác của góc B cắt AC ở D. Trên tia đối của BD lấy E sao cho BE = AC. Trên tia đối của CB lấy K sao cho CK = AB. Chứng minh AE = AK.
Bài 8: Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Vẽ F sao cho E là trung điểm của DF. Chứng minh:
a) DB = CF
b) Hai tam giác BDC và FCD bằng nhau
c) DE // BC và DE = 1/2BC
Bài 9: Cho tam giác ABC. Trên AB lấy D à E sao cho AD = BE. Qua D, E vẽ các đường thẳng song song với BC, chúng cắt AC theo thứ tự ở M và N. Chứng minh BC = DM + EN.
Bài 10: Cho tam giác ABC có góc A = 600. Các tia phân giác của các góc B và C cắt nhau ở I và cắt AC, AB theo thứ tự ở D và E. Chứng minh ID = IE.
Bài 11: Cho tam giác ABC vuông tại A có AB = AC. Lấy D thuộc AB, E thuộc AC sao cho AD = AE. Đường thẳng đi qua D vuông góc với BE cắt CA ở K. Chứng minh AK = AC?
Bài 12: Cho tam giác ABC có góc A nhọn, AB = AC. Qua A kẻ đường thẳng xy sao cho B và C nằm cùng phía với xy. Vẽ BD vuông góc xy ở D, CE vuông góc xy ở E.
a) Chứng minh hai tam giác BAD và ACE bằng nhau.
b) Chứng minh DE = BD + CE
Bài 13: Cho tam giác ABC có góc A nhọn. Trên nửa mặt phẳng bờ AB chứ C, vẽ AD vuông góc với AB, AD = AB. Trên nửa mặt phẳng bờ AC chứa B, vẽ AE vuông góc AC, AE = AC. Kẻ AH vuông góc ED tại H. Chứng minh AH đi qua trung điểm của BC?
Bài 14: Gọi D là trung điểm cạnh BC của tam giác ABC. Qua D kẻ đường thẳng vuông góc với đường phân giác trong của góc BAC cắt AB, AC lần lượt ở M và N.
a) Chứng minh BM = CN
b) Cho biết AB = c, AC = b. Tính độ dài các đoạn thẳng AM, BM.
Bài 15: Cho tam giác ABC có AB = AC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho AM = MD
a. Chứng minh rằng tam giác ABM bằng tam giác DCM.
b. Chứng minh AB song song với DC.
c. Chứng minh AM vuông góc với BC.
Bài 16: Cho tam giác ABC vuông tại A, AB = AC. Qua A vẽ đường thẳng d sao cho B nằm cùng phía đối với đường thẳng d. Kẻ BH và CK vuông góc với d. Chứng minh:
a. AH = CK
b. HK = BH + CK
Bài 17: Cho góc nhon xOy. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OB = OA. Trên tia Ax lấy điểm C, trên tia By lấy điểm D sao cho AC = BD
a. Chứng minh AD = BC
b. Gọi E là giao điểm của AD và BC. Chứng minh tam giác EAC bằng tam giác EBD
c. Chứng minh OE là phân giác góc xOy
Bài 18: Cho tam giác ABC có 3 góc đều nhọn, đường cao AH vuông góc với BC tại H. Trên tia đối của tia HA lấy điểm D sao cho HA = HD
a. Chứng minh BC và CB lần lượt là tia phân giác của các góc ABD và ACD.
b. Chứng minh CA = CD và DB = BA
c. Cho góc ACB bằng 45o tính góc ADC.

biết kẻ hình nắm rõ kiến thức và vận dụng tốt những kiến thức

\(\frac{2}{4}=\frac{3}{6}=\frac{2+3}{4+6}\)
\(\frac{2}{4}=\frac{3}{6}=\frac{2-3}{4-6}\)
\(\Rightarrow\frac{2+3}{4+6}=\frac{2-3}{4-6}\)


Tham khảo
Bài 13 (trang 32 SGK Toán 7 tập 2): Tính tích các đơn thức sau rồi tìm bậc của đơn thức thu được:
Lời giải:
a)
Bậc của đơn thức trên là tổng số mũ của các biến x và y
Số mũ của biến x là 3 ; số mũ của biến y là 4
⇒ Bậc của đơn thức đó là 3+4=7.
b)
Bậc của đơn thức trên là tổng số mũ của các biến x và y
Số mũ của biến x là 6 ; số mũ của biến y là 6.
⇒ Bậc của đơn thức đó là 6+6 = 12
Tham khảo
a)
Bậc của đơn thức trên là tổng số mũ của các biến x và y
Số mũ của biến x là 3 ; số mũ của biến y là 4
⇒ Bậc của đơn thức đó là 3+4=7.
b)
Bậc của đơn thức trên là tổng số mũ của các biến x và y
Số mũ của biến x là 6 ; số mũ của biến y là 6.
⇒ Bậc của đơn thức đó là 6+6 = 12

 giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1
giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1
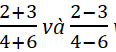 với các tỉ số trong tỉ lệ thức đã cho.
với các tỉ số trong tỉ lệ thức đã cho.
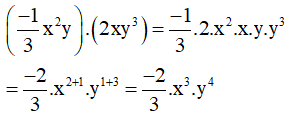
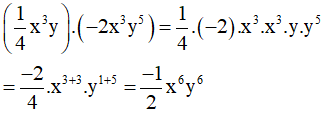
where is câu hỏi??