LC
6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
0
TT
2
AB
2
18 tháng 7 2016
x^2 + 2y^2 - 2y - 2xy + 1 = (x^2 - 2xy + y^2) + (y^2 - 2y + 1) = (x - y)^2 + (y - 1)^2
18 tháng 7 2016
\(x^2+2y^2-2y-2xy+1\)
\(=x^2-2xy+y^2+y^2-2y+1\)
\(=\left(x-y\right)^2+\left(y-1\right)^2\)
\(=\left(x-y\right)^2-\left(1-y\right)^2\)
\(=\left(x-y-1+y\right)\left(x-y+1-y\right)\)
\(=\left(x-1\right)\left(x-2y+1\right)\)
BN
3
3 tháng 1 2017
Gửi Thắng Nguyễn: Mình không biết tại sao lại ko phân tích được?
CM
8 tháng 4 2019
Ta để ý : x2 – 1 = (x – 1)(x + 1)
Do đó ta cần chia cả tử và mẫu của phân thức thứ nhất cho x – 1.
Mà ta có :
x5 – 1 = x5 – x4 + x4 – x3 + x3 – x2 + x2 – x + x – 1
= x4(x – 1) + x3(x – 1) + x2(x – 1) + x(x – 1) + (x – 1)
= (x – 1)(x4 + x3 + x2 + x + 1)
Do đó :
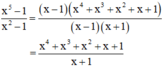
Vậy đa thức cần điền là x4 + x3 + x2 + x + 1.
CM
15 tháng 8 2019
Ta có:
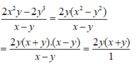
Vậy đa thức cần điền vào chỗ trống là 2y(x+ y)
Chọn đáp án D
22 tháng 4 2017
tính chất quan trọng phần thức với
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow ad=bc\Rightarrow c=\dfrac{ad}{b}\)áp vào
\(\dfrac{x^5-1}{x^2-1}=\dfrac{A}{x+1}\Rightarrow A=\dfrac{\left(x^5-1\right)\left(x+1\right)}{x^2-1}\) {x khác +-1}
\(A=\dfrac{\left(x^5-1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{\left[\left(x-1\right)\left(x^4+x^3+x^2+x+1\right)\right]\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\left(x^4+x^3+x^2+x+1\right)\)
Vậy đa thức cần điền là
\(A=\left(x^4+x^3+x^2+x+1\right)\)
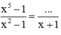
\(a,=x\left(\frac{3}{7}x+6+xy\right)\)
\(b,=\left(x+3y\right)\left(3x-6xy\right)=\left(x+3y\right).3x\left(1-2y\right)\)
\(c,=x\left(x+y\right).\left(-5\right)\left(x+y\right)=\left(x+y\right)\left[x.\left(-5\right)\right]\)
\(d,=3\left(x-y\right)+5x\left(x-y\right)=\left(x-y\right)\left(3+5x\right)\)
\(B3.a,x\left(1+6x\right)=0\)
\(Th1:x=0\)
\(Th2:1+6x=0=>x=-\frac{1}{6}\)
Vậy \(x\in\left\{0;-\frac{1}{6}\right\}\)
\(b,\left(x+3\right)\left(2-x\right)=0\)
\(Th1:x+3=0=>x=-3\)
\(Th2:2-x=0=>x=2\)
Vậy \(x\in\left\{-3;2\right\}\)
\(c,5x\left(x-2\right)+\left(x-2\right)=0\)
\(\left(x-2\right)\left(5x+1\right)=0\)
\(Th1:x-2=0=>x=2\)
\(5x +1=0=>x=-\frac{1}{5}\)
Vậy \(x\in\left\{-\frac{1}{5};2\right\}\)