Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(AB=5\left(cm\right)< CD=k^2\)
\(MN=11\left(cm\right)>CD=k^2\)
\(\Rightarrow CD=k^2=9\left(cm\right)\)

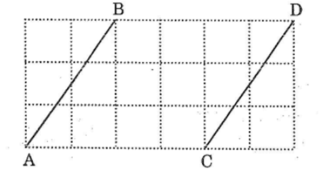
Gọi giao điểm của đường kẻ ngang đi qua điểm A và đường kẻ dọc đi qua điểm B cắt nhau tại H.
Giao điểm đường kẻ ngang đi qua C và đường kẻ dọc đi qua D là K
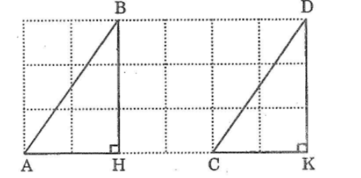
Xét ΔAHB và ΔCKD, ta có:
AH = CK (bằng 2 ô vuông)
∠(AHB) =∠(CKD) =90o
BH = DK (bằng 3 ô vuông)
Suy ra ΔAHB= ΔCKD (c.g.c)
⇒ AB = CD (hai cạnh tương ứng) và ∠(BAH) =∠(DCK) (hai góc tương ứng)
Hai đường thẳng AB Và CD cắt đường thẳng AK có 2 góc ∠(BAH) và ∠(DCK) ̂ở vị trí đồng vị bằng nhau nên AB // CD.

Ak tính bằng niềm tin và hi vọng nha bạn
Chúc bạn thành công với cách này!

ab =2cd thì abcd chia hết cho 67 abcd=ab.100+cd =2cd.200+cd =201.cd=67.3.cd => chia hết mẹ nó cho cd


1/nối AC
Do AB//CD=>BAC=ACD(so le trong)
Do AD//BC=>ACB=DAC(so le trong)
Xét ∆ABC và ∆ACD
ACB=DAC(chứng minh trên)
BAC=DAC(chứng minh trên)
AC chung
Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)
AD=BC(cặp cạnh tương ứng)
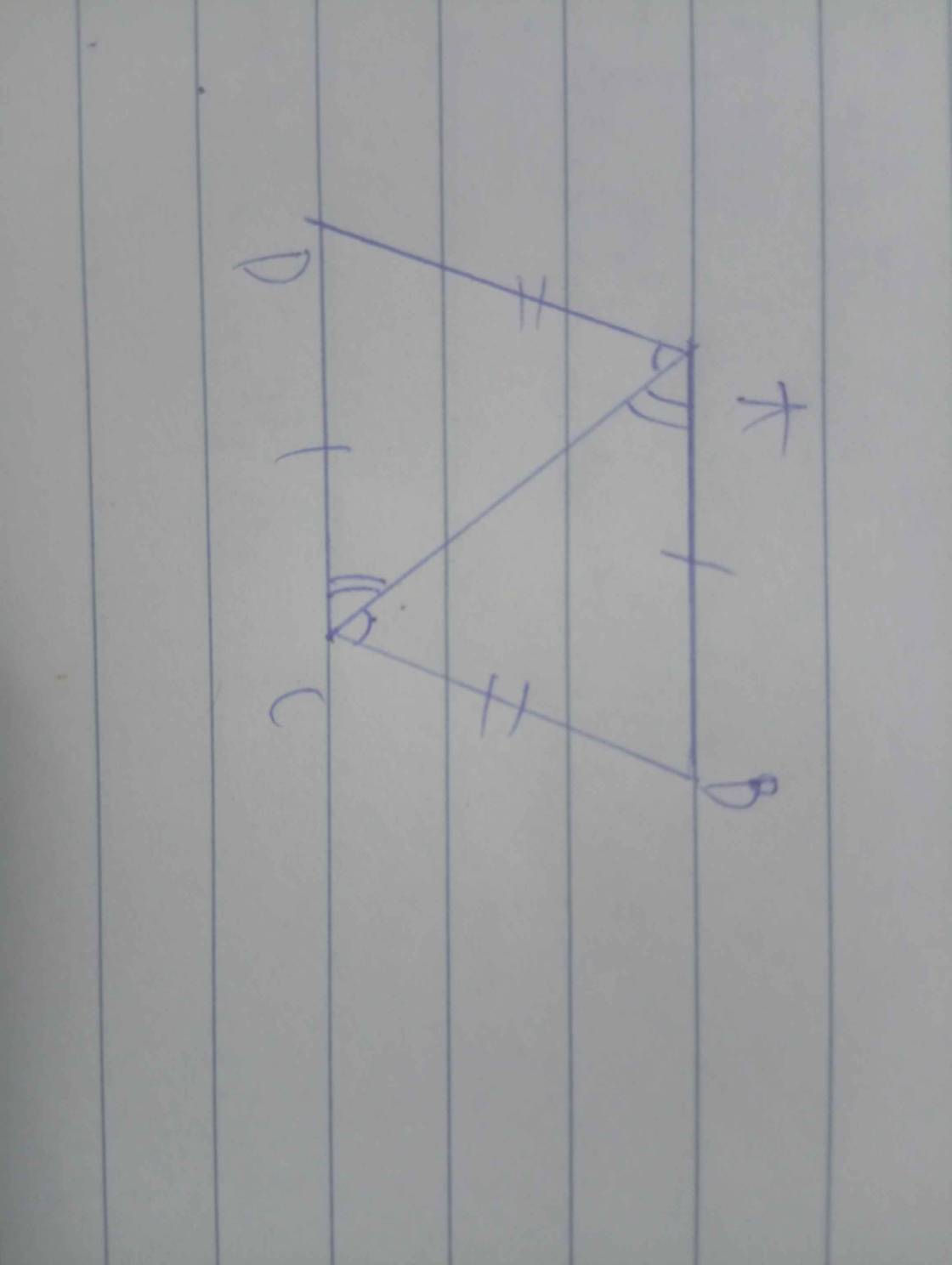

Xét ∆AHB và ∆ CKD có:
HB=KD.
ˆAHB=ˆCKD
AH=CK
=> ∆ AHB = ∆ CKD(c.g.c)
=> AB=CD.( 2 canh tương ứng)
tương tự ∆ CEB = ∆ AFD(c.g.c)
=> BC=AD.
b) ∆ABD và ∆CDB có:
AB=CD(CMT)
BC=AD(CMT)
BD chung.
=> ∆ABD=∆CDB(c.c .c)
=> ˆABD^=ˆCDB( 2 góc tương ứng)
=> AB // CD( hai góc so le trong bằng nhau)