Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\left\{{}\begin{matrix}3x+y=3\\2x-y=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x=10\\2x-y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2x-7=2\cdot2-7=-3\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là (x,y)=(2;-3)
b) Ta có: \(7x^2-2x+3=0\)
a=7; b=-2; c=3
\(\Delta=\left(-2\right)^2-4\cdot7\cdot3=4-84=-80< 0\)
Suy ra: Phương trình vô nghiệm
Vậy: \(S=\varnothing\)

Bài 2:
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(2x^2=-x+3\)
\(\Leftrightarrow2x^2+x-3=0\)
\(\Leftrightarrow2x^2-2x+3x-3=0\)
\(\Leftrightarrow2x\left(x-1\right)+3\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Thay x=1 vào hàm số \(y=2x^2\), ta được:
\(y=2\cdot1^2=2\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số \(y=2x^2\), ta được:
\(y=2\cdot\left(-\dfrac{3}{2}\right)^2=2\cdot\dfrac{9}{4}=\dfrac{9}{2}\)
Vậy: Tọa độ giao điểm của (p) và (D) là (1;2) và \(\left(-\dfrac{3}{2};\dfrac{9}{2}\right)\)

chú ý\(x=\sqrt{x}^2\) tương tự với y , và các số tự nhiên dương
\(A=\frac{\sqrt{x}^2+2\sqrt{x}-3}{\sqrt{x}-1}=\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-1\right)}=\sqrt{x}+3\)
\(B=\frac{\left(2\sqrt{y}\right)^2+3\sqrt{y}-7}{4\sqrt{y}+7}=\frac{\left(\sqrt{y}-1\right)\left(4\sqrt{y}+7\right)}{4\sqrt{y}+7}=\sqrt{y}-1\)
\(C=\frac{\sqrt{x}^2\sqrt{y}-\sqrt{y}^2\sqrt{x}}{\sqrt{x}-\sqrt{y}}=\frac{\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)}{\sqrt{x}-\sqrt{y}}=\sqrt{xy}\)
\(D=\frac{\sqrt{x}^2-3\sqrt{x}-4}{\sqrt{x}^2-\sqrt{x}-12}=\frac{\left(\sqrt{x}-4\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-4\right)\left(\sqrt{x}+3\right)}=\frac{\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+3\right)}\)
\(E=\sqrt{1+2\sqrt{5}+5}+\sqrt{\sqrt{5}-2\sqrt{5}+1}=\sqrt{\left(1+\sqrt{5}\right)^2}+\sqrt{\left(\sqrt{5}-1\right)^2}\)
=>\(E=1+\sqrt{5}+\sqrt{5}-1=2\sqrt{5}\)
CÂU CUỐI chưa làm đc
ý cuối cùng này :
\(D=\sqrt{13-4\sqrt{10}}+\sqrt{13+4\sqrt{10}}\)lấy bình phương 2 vế ta có
\(D^2=13-4\sqrt{10}+13+4\sqrt{10}+2\sqrt{13-4\sqrt{10}}\sqrt{13+4\sqrt{10}}\)
\(D^2=26+2\sqrt{13^2-16\sqrt{10}^2}\Leftrightarrow D^2=26+2\sqrt{9}\)
\(D^2=32\Leftrightarrow D=\sqrt{32}=4\sqrt{2}\)

\(\frac{1}{2}x+0y=12\Leftrightarrow\frac{1}{2}x=12\Leftrightarrow x=24\)
Vậy nghiệm của phương trình trên được biểu diễn bởi đường thẳng có phương trình là $x=24$ Do đó bạn xem lại câu hỏi có nhầm gì không nhé!

\(a,\dfrac{x+2\sqrt{x}-3}{\sqrt{x}-1}\)
\(\Leftrightarrow\dfrac{x+3\sqrt{x}-\sqrt{x}-3}{\sqrt{x}-1}\)
\(\Leftrightarrow\dfrac{\sqrt{x}.\left(\sqrt{x}+3\right)-\left(\sqrt{x}+3\right)}{\sqrt{x}-1}\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\)
\(\Rightarrow\sqrt{x}+3\)
\(b,\dfrac{4y+3\sqrt{y}-7}{4\sqrt{y}+7}\)
\(\Leftrightarrow\dfrac{4y+7\sqrt{y}-4\sqrt{y}-7}{4\sqrt{y}+7}\)
\(\Leftrightarrow\dfrac{\sqrt{y}.\left(4\sqrt{y}\right)-\left(4\sqrt{y}+7\right)}{4\sqrt{y}+7}\)
\(\Leftrightarrow\dfrac{\left(4\sqrt{y}+7\right).\left(\sqrt{y}-1\right)}{4\sqrt{y}+7}\)
\(\Rightarrow\sqrt{y}-1\)
\(c,\dfrac{x\sqrt{y}-y\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
\(\Leftrightarrow\dfrac{\sqrt{xy}.\left(\sqrt{x}-\sqrt{y}\right)}{\sqrt{x}-\sqrt{y}}\)
\(\Rightarrow\sqrt{xy}\)
\(d,\dfrac{x-3\sqrt{x}-4}{x-\sqrt{x}-12}\)
\(\Leftrightarrow\dfrac{x+\sqrt{x}-4\sqrt{x}-4}{x+3\sqrt{x}-4\sqrt{x}-12}\)
\(\Leftrightarrow\dfrac{\sqrt{x}.\left(\sqrt{x}+1\right)-4\left(\sqrt{x}+1\right)}{\sqrt{x}.\left(x+3\right)-4\left(\sqrt{x}+3\right)}\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}+1\right).\left(\sqrt{x}-4\right)}{\left(\sqrt{x}+3\right).\left(\sqrt{x}-4\right)}\)
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\)
\(\Rightarrow\dfrac{x-2\sqrt{x}-3}{x-9}\)
\(e,\dfrac{1+\sqrt{x}+\sqrt{y}+\sqrt{xy}}{1+\sqrt{4}}\)
\(\Leftrightarrow\dfrac{1+\sqrt{x}+\sqrt{y}+\sqrt{xy}}{1+2}\)
\(\Rightarrow\dfrac{1+\sqrt{x}+\sqrt{y}+\sqrt{xy}}{3}\)

a: ĐKXĐ: x<>-1 và y<>-1
\(\left\{{}\begin{matrix}\dfrac{2x}{x+1}+\dfrac{y}{y+1}=2\\\dfrac{x}{x+1}+\dfrac{3}{y+1}=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2x+2-2}{x+1}+\dfrac{y+1-1}{y+1}=2\\\dfrac{x+1-1}{x+1}+\dfrac{3}{y+1}=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2-\dfrac{2}{x+1}+1-\dfrac{1}{y+1}=2\\1-\dfrac{1}{x+1}+\dfrac{3}{y+1}=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{-2}{x+1}+\dfrac{-1}{y+1}=2-3=-1\\\dfrac{1}{x+1}-\dfrac{3}{y-1}=1+1=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{-2}{x+1}+\dfrac{-1}{y+1}=-1\\\dfrac{2}{x+1}-\dfrac{6}{y-1}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{7}{y-1}=3\\\dfrac{1}{x+1}-\dfrac{3}{y-1}=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y-1=-\dfrac{7}{3}\\\dfrac{1}{x+1}-3:\dfrac{-7}{3}=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-\dfrac{4}{3}\\\dfrac{1}{x+1}+3\cdot\dfrac{3}{7}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{4}{3}\\\dfrac{1}{x+1}=2-\dfrac{9}{7}=\dfrac{5}{7}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-\dfrac{4}{3}\\x+1=\dfrac{7}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{4}{3}\\x=\dfrac{2}{5}\end{matrix}\right.\left(nhận\right)\)
b: ĐKXĐ: y<>0 và y<>-12
\(\left\{{}\begin{matrix}\dfrac{x}{y}-\dfrac{x}{y+12}=1\\\dfrac{x}{y+12}-\dfrac{x}{y}=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{x}{y}-\dfrac{x}{y+12}=1\\\dfrac{x}{y}-\dfrac{x}{y+12}=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0\cdot\dfrac{x}{y+12}=3\left(vôlý\right)\\\dfrac{x}{y}-\dfrac{x}{y+12}=1\end{matrix}\right.\)
Vậy: \(\left(x,y\right)\in\varnothing\)
d: ĐKXĐ: \(\left\{{}\begin{matrix}x< >1\\y< >1\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\dfrac{2x}{y-1}+\dfrac{3y}{x-1}=1\\\dfrac{2y}{x-1}-\dfrac{5x}{y-1}=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2x}{y-1}+\dfrac{3y}{x-1}=1\\\dfrac{5x}{y-1}-\dfrac{2y}{x-1}=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{4x}{y-1}+\dfrac{6y}{x-1}=2\\\dfrac{15x}{y-1}-\dfrac{6y}{x-1}=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{19x}{y-1}=-4\\\dfrac{2x}{y-1}+\dfrac{3y}{x-1}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{x}{y-1}=\dfrac{-19}{4}\\2\cdot\dfrac{-19}{4}+\dfrac{3y}{x-1}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=-19\left(y-1\right)\\\dfrac{3y}{x-1}=1+\dfrac{19}{2}=\dfrac{21}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+19y=19\\\dfrac{y}{x-1}=\dfrac{7}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+19y=19\\7x-7=2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+19y=19\\7x-2y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x+38y=38\\133x-38y=133\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}141x=171\\7x-2y=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{171}{141}\\2y=7x-7=\dfrac{70}{47}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{171}{141}=\dfrac{57}{47}\\y=\dfrac{35}{47}\end{matrix}\right.\left(nhận\right)\)
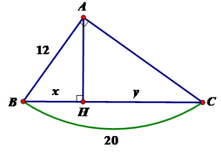
Đáp án C
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Vậy x = 7,2; y = 12,8