K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
22 tháng 7 2023
1/
\(N=1.\left(2-1\right)+2\left(3-1\right)+3\left(4-1\right)+...+99\left(100-1\right)=\)
\(=\left(1.2+2.3+3.4+...+99.100\right)-\left(1+2+3+...+99\right)=\)
Đặt
\(A=1.2+2.3+3.4+...+99.100\)
\(3A=1.2.3+2.3.3+3.4.3+...+99.100.3=\)
\(=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+99.100.\left(101-98\right)=\)
\(=1.2.3-1.2.3+2.3.4-2.3.4+3.4.5-...-98.99.100+99.100.101=\)
\(=99.100.101\Rightarrow A=\dfrac{99.100.101}{3}=33.100.101\)
Đặt
\(B=1+2+3+...+99=\dfrac{99.\left(1+99\right)}{2}=4950\)
\(\Rightarrow N=A-B\)
2/
Số hạng cuối cùng là 10000 hoặc 1000000 mới làm được
\(A=1^2+2^2+3^2+...+100^2\)
Tính như câu 1
3/ Làm như bài 4
4/
\(S=1^2+3^2+5^2+...+99^2=\)
\(=1.\left(3-2\right)+3\left(5-2\right)+5\left(7-2\right)+...+99\left(101-2\right)=\)
\(=\left(1.3+3.5+5.7+...+99.101\right)-2\left(1+3+5+...+99\right)\)
Đặt
\(B=1+3+5+...+99=\dfrac{50.\left(1+99\right)}{2}=2500\)
Đặt
\(A=1.3+3.5+5.7+...+99.101\)
\(6A=1.3.6+3.5.6+3.7.6+...+99.101.6=\)
\(=1.3.\left(5+1\right)+3.5.\left(7-1\right)+5.7.\left(9-3\right)+...+99.101.\left(103-97\right)=\)
\(=1.3+1.3.5-1.3.5+3.5.7-3.5.7+5.7.9-...-97.99.101+99.101.103=\)
\(=3+99.101.103\Rightarrow A=\dfrac{3+99.101.103}{6}\)
\(\Rightarrow S=A-2B\)
GH
Gia Hân
VIP
22 tháng 7 2023
Bài 1:
\(N=1^2+2^2+3^3+...+99^2\)
\(N=1.1+2.2+3.3+...+99.99\)
\(N=1.\left(2-1\right)+2.\left(3-1\right)+3.\left(4-1\right)+...+99.\left(100-1\right)\)
\(N=1.2-1+2.3-2+3.4-3+...+99.100-99\)
\(N=\left(1.2+2.3+3.4+...+99.100\right)-\left(1+2+3+...+99\right)\)
Đặt \(\left\{{}\begin{matrix}A=1.2+2.3+3.4+...+99.100\\B=1+2+3+...+99\end{matrix}\right.\)
+) Tính \(A=1.2+2.3+3.4+...+99.100\)
Ta có:
\(3A=1.2.3+2.3.3+3.4.3+...+99.100.3\)
\(3A=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+99.100.\left(101-98\right)\)
\(3A=1.2.3+2.3.4-1.2.3+3.4.5-2.3.4+...+99.100.101-98.99.100\)
\(3A=99.100.101\)
\(\Rightarrow A=\dfrac{99.100.101}{3}=333300\)
+) Tính \(B=1+2+3+...+99\)
\(B\) có số số hạng là: \(\dfrac{99-1}{1}\) + 1 = 99 (số hạng)
\(\Rightarrow B=\dfrac{\left(99+1\right).99}{2}=4950\)
\(\Rightarrow N=A-B=333300-4950=328350\)
\(\Rightarrow N=328350\)
18 tháng 9 2017
A) Có: ( 100 - 7 ) : 3 +1= 32 [ ( số cuối - số đầu ) : khoảng cách cộng 1 ]
b) Số hạng thứ 24 là: ( 24 - 1 ) x 3 + 7 =76 [ ( n-1 ) x khoảng cách ]
c) S = ( 100 + 7 ) x 32 : 2 = 1712 [ ( số cuối + số đầu ) x số các số hạng : 2)
k mik nha
N
0
25 tháng 6 2016
a) Số chẵn thứ 2015 là:
\(\left(2015-1\right).2+0=4028\)
2015 số chẵn đầu tiên tạo thành dãy : 0 ; 2 ; 4 ; 6 ; ... ; 4028
Tổng của 2015 số chẵn đầu tiên là:
\(\left(4208+0\right).2015:2=4058210\)
b) Số chia hết 3 thứ 2015 là:
\(\left(2015-1\right).3+0=6042\)
2015 số chia hết cho 3 đầu tiên tạo thành dãy: 0 ; 3 ; 6 ; 9 ; ... ; 6042
tổng của 2015 chia hết cho 3 đầu tiên là:
\(\left(6042+0\right).2015:2=6087315\)
c) số tự nhiên chia 3 dư 1 thứ 15 là :
\(\left(15-1\right).3+1=43\)
15 số tự nhiên đầu tiên chia 3 dư 1 tạo dãy: 1 ; 4 ; 7 ; 10 ; ... ; 43
tổng 15 số tự nhiên đầu tiên chia 3 dư 1 là :
\(\left(43+1\right).15:2=330\)
LP
0
NK
5
VN
26 tháng 10 2017
a)số các số hạng trong S là:
(98-2):2+1=49(số)
Tổng S là:
(2+98).45:2=2250
b) số các số hạng là:
(99-1):2+1=50(số)
tổng S là:
(99+1).50:2=2500
M
0
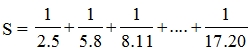
\(S=\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+...+\frac{1}{17.20}\)
\(S=3.\left(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+\frac{1}{8}-\frac{1}{11}+...+\frac{1}{17}-\frac{1}{20}\right)\)
\(S=3.\left(\frac{1}{2}-\frac{1}{20}\right)\)
\(S=3.\frac{9}{20}=\frac{27}{20}\)