M
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 3 2022
Ta có: \(A=\frac{2020}{2021}+\frac{2021}{2022}\)
\(\Rightarrow A=\frac{2021}{2021}-\frac{1}{2021}+\frac{2022}{2022}-\frac{1}{2022}\)
\(\Rightarrow A=1-\frac{1}{2021}+1-\frac{1}{2022}\)
\(\Rightarrow A=1+1-\frac{1}{2021}-\frac{1}{2022}\)
\(\Rightarrow A=2-\frac{1}{2021}-\frac{1}{2022}\)
\(\Rightarrow A=2-\frac{1}{2021\cdot2022}\)
\(B=\frac{2020+2021}{2021+2022}\)
\(\Rightarrow B=\frac{2021+2022}{2021+2022}-\frac{2}{2021+2022}\)
\(\Rightarrow B=1-\frac{2}{2021+2022}\)
\(\Rightarrow B=1-\frac{2}{4043}\)
Vậy ta sẽ so sánh:
\(1-\frac{1}{2021\cdot2022};\frac{2}{4043}\)
Vì \(2021\cdot2022>4043\)nên \(\frac{1}{2021\cdot2022}< \frac{2}{4043}\)vậy \(1-\frac{1}{2021\cdot2022}>\frac{2}{4043}\)
\(\Rightarrow\frac{2020}{2021}+\frac{2021}{2022}>\frac{2020+2021}{2021+2022}\)
\(\Rightarrow A>B\)
2
16 tháng 11 2021
\(A=3+3^2+3^3+...+3^{2021}\)
\(\Rightarrow A+1=1+3+3^2+3^3+...+3^{2021}\)
\(A+1=\left(1+3+3^2\right)+\left(3^3+3^4+3^5\right)+...+\left(3^{2019}+3^{2020}+3^{2021}\right)\)
\(A+1=\left(1+3+3^2\right)+3^3\left(1+3+3^2\right)+...+3^{2019}\left(1+3+3^2\right)\)
\(A+1=13.3^3.13+...+3^{2019}.13\)
\(A+1=13\left(1+3^3+...+3^{2019}\right)\)
\(\Rightarrow A+1⋮13\)
\(\Rightarrow A:13d\text{ư}12\)
DN
16 tháng 11 2021
ta có :
A = 3 + 32 + ( 33 +34 + 35 ) + ( 36 + 37 + 38 ) + ... + ( 32019 +32020 + 32021 )
Đặt B = ( 33 +34 + 35 ) + ( 36 + 37 + 38 ) + ... + ( 32019 +32020 + 32021 )
B = 351 + ( 33 .33 + 33 . 34 + 33 .35 ) + .... + ( 32016 .33 + 32016 .34 + 32016 . 35 )
B = 351 + 351 . 33 + ... + 351 .32016
B = 351 ( 1 + 33 + ... + 32016 ) \(⋮\)11
Thay B vào A => 3 + 32 + B chia 11 dư 3 + 32
ta có 3 + 32 = 3 + 9
= 12
mà 12 \(\equiv\)-1 ( mod 13 )
Vậy A chia 13 dư -1
học CLB toán à : > ? có bài nào hay hay ib mk nha ^^
Học tốt
#Gấu
SC
8
28 tháng 7 2016
2005 x 1789 - 2005 - 788 x 2005
= 2005 x 1789 - 2005 x 1 - 2005 x 788
= 2005 x ( 1789 - 1 - 788 )
= 2005 x 1000
= 2005000
28 tháng 7 2016
2005.1789-2005-788.2005
=2005.1789-2005.1-788.2005
=2005.(1789-1-788)
=2005.1000
=2005000
12 tháng 12 2022
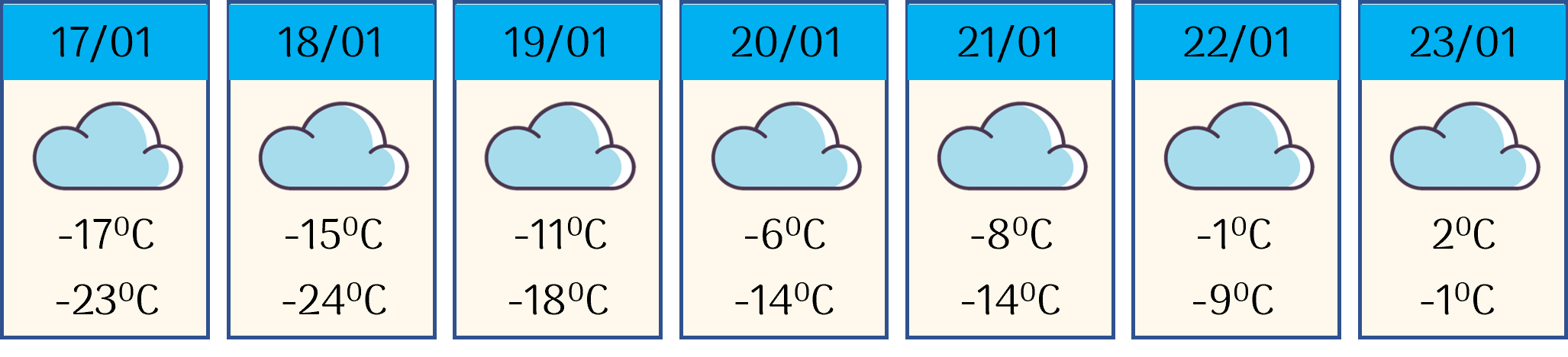
a) nhiệt độ cao nhất: -1°C
nhiệt độ thấp nhất: -9°C
b)8°C
TA
19 tháng 12 2022
a)
+ Nhiệt độ cao nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga trong ngày 22/1/2021 là -1^{\circ}−1∘C.
+ Nhiệt độ thấp nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga trong ngày 22/1/2021 là -9^{\circ}−9∘C.
b) Chênh lệch giữa nhiệt độ cao nhất và nhiệt độ thấp nhất ở Thủ đô Mát-xcơ-va của Liên bang Nga trong ngày 22/1/2021 là -1-(-9)=-1+9=8^{\circ}−1−(−9)=−1+9=8∘C.
DD
Đoàn Đức Hà
Giáo viên
8 tháng 5 2021
Xét hai số \(2022!+1\)và \(2022!+2022\). Hai số này có hiệu là \(2021\), ta sẽ chứng minh không tồn tại số nguyên tố nào nằm giữa hai số này.
Thật vậy, ta có \(2022!+k\)với \(1< k\le2022\)luôn chia hết cho \(k\)mà \(2022!+k>k\)nên số đó không là số nguyên tố.
Vậy tồn tại hai số nguyên tố liên tiếp mà hiệu của chúng lớn hơn \(2021\).
DD
Đoàn Đức Hà
Giáo viên
8 tháng 5 2021
\(3^x-9y+113=6y^4\)
Với \(x\ge1\)ta có: \(3^x⋮3,9y⋮3,6y^4⋮3,113⋮̸3\)nên phương trình vô nghiệm.
Với \(x=0\)có: \(6y^4+9y-114=0\)
có nghiệm nguyên duy nhất \(y=2\).
Vậy phương trình có nghiệm duy nhất \(\left(0,2\right)\).
18 tháng 7 2017
Số tập hợp còn là 4
\(\left(x+2\right)\left(x-5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\x-5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=5\end{cases}}}\)
18 tháng 7 2017
câu 1: số tập hợp con của F là 4 câu 2: (x+2)(x-5)=0 => x+2=0 hoặc x-5=0 => x=-2 hoặc x=5
25 tháng 7 2016
a, Vì có 2008 số, có 2 số riêng nên có 2006 số theo cặp, tức có 1003 cặp
Mỗi cặp có giá trị bằng -1
-1+2-3+4-5+...............+2006-2007+2008=(-1X1003)+2008=-1003+2008=1005
SS
25
-2021 . 20222022 + 2022 .20212021
= -2021 . 2022. 10001 + 2022.2021. 10001
= 0
-2021 . 20222022 + 2022 . 20212021
= (-2021) . (20222022 - 2022 . 10001)
= (-2021) . (20222022 - 20222022)
= (-2021) . 0
= 0