
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=65^2+60\cdot65+15^2-20^2\)
\(=65^2+2\cdot65\cdot30+30^2-1075\)
\(=95^2-1075\)
=7950

3: Đặt x+3=a
Ta có: (x+3)(x+4)(x+5)=x
⇔a(a+1)(a+2)=a-3
⇔\(a^3+3a^2+2a-a+3=0\)
\(\Leftrightarrow a^3+3a^2+a+3=0\)
\(\Leftrightarrow a^2\left(a+3\right)+\left(a+3\right)=0\)
\(\Leftrightarrow\left(a+3\right)\left(a^2+1\right)=0\)(1)
Ta có: \(a^2\ge0\forall a\)
\(\Rightarrow a^2+1\ge1>0\forall a\)(2)
Từ (1) và (2) suy ra a+3=0
hay \(x+6=0\)
⇔x=-6
Vậy: x=-6

Ta có:
(10a + 5)2 = (10a)2 + 2.10a.5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25
Đặt A = a.(a + 1). Khi đó ta có:
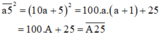
Do vậy, để tính bình phương của một số tự nhiên có dạng 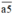 , ta chỉ cần tính tích a.(a + 1) rồi viết 25 vào đằng sau kết quả vừa tìm được.
, ta chỉ cần tính tích a.(a + 1) rồi viết 25 vào đằng sau kết quả vừa tìm được.
Áp dụng:
252 = 625 (Vì 2.3 = 6)
352 = 1225 (Vì 3.4 = 12)
652 = 4225 (Vì 6.7 = 42)
752 = 5625 (Vì 7.8 = 56)

b) Ta có: \(x^3+4x+5=0\)
\(\Leftrightarrow x^3-x+5x+5=0\)
\(\Leftrightarrow x\left(x^2-1\right)+5\left(x+1\right)=0\)
\(\Leftrightarrow x\left(x+1\right)\left(x-1\right)+5\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-x+5\right)=0\)
mà \(x^2-x+5>0\forall x\)
nên x+1=0
hay x=-1
Vậy: S={-1}
a)x2-(x+3)(3x+1)=9
⇔(x-3)(x+3)-(x+3)(3x+1)=0
⇔x+3=0 hoặc 3x+1=0
1.x+3=0 ⇔x=-3
2.3x+1=0⇔x=-1/3
phương trình có 2 nghiệm x=-3 và x=-1/3

Ta có:
(10a + 5)2 = (10a)2 + 2.10a.5 + 52
= 100a2 + 100a + 25
= 100a(a + 1) + 25
Đặt A = a.(a + 1). Khi đó ta có:
Do vậy, để tính bình phương của một số tự nhiên có dạng 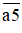

Giải phương trình
a, x2 - (x-3)(3x+1) = 9
\(\Leftrightarrow\) x2 - 3x2 + 8x +3 = 9
\(\Leftrightarrow\) -2x2 + 8x - 6 = 0
\(\Leftrightarrow\) \(\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
b, (x+14)3 - (x+12)3 =1352
\(\Leftrightarrow\) (x+14-x-12)[(x+14)2 + (x+14)(x+12) + (x+12)2 ] = 1352
\(\Leftrightarrow\) 6(x2 + 28x + 196 + x2 + 26x + 168 + x2 +24x +144) =1352
\(\Leftrightarrow\) 18x2 +468x + 3048 = 1352
Pt nghiệm vô tỉ
a) \(x^2-\left(x-3\right)\left(3x+1\right)=9\)
\(\Leftrightarrow x^2-9-\left(x-3\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+3\right)-\left(x-3\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+3-3x-1\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(2-2x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\2x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
Vậy nghiệm của pt x = 3 hoặc x = 1
Tập nghiệm của phương trình (x + 14)3 - (x + 12)3 = 1352 là:
A. 2 B. {-28; 2} C. 2 và -28 D. {2; 28}

+) Cách 1: Em thay x= 2; 28 ; -28 vào phương trình xem cái nào là nghiệm
=> Đáp án cần chọn
+) Cách 2: ( Cách em nên học )
Đăt \(t=x+\frac{14+12}{2}=x+13\)
Ta có phương trình: \(\left(t+1\right)^3-\left(t-1\right)^3=1352\)
<=> \(\left(t^3+3t^2+3t+1\right)-\left(t^3-3t^2+3t-1\right)=1352\)
<=> \(6t^2+2=1352\)
<=> \(t^2=225\) <=> t = 15 hoặc t = - 15
+) Với t = 15
ta có: 15 = x + 13 <=> x = 2
+) Với t = - 15
ta có: -15 = x + 13 <=> x = -28
Vậy S = { 2; -28 }
Vậy là đáp án B

Ta có:\(\frac{x+21}{1998}-\frac{x+25}{1994}+\frac{x+63}{652}-\frac{x+75}{648}=0\)
\(\Rightarrow\frac{x+21}{1998}-\frac{x+25}{1994}+\frac{x+63}{652}-\frac{x+75}{648}+4-4=0\)
\(\Rightarrow\frac{x+21}{1998}+1-\frac{x+25}{1994}-1+\frac{x+63}{652}+3-\frac{x+75}{648}-3=0\)
\(\Rightarrow\frac{x+2019}{1998}-\frac{x+2019}{1994}-\frac{x+2019}{652}+\frac{x+2019}{648}=0\)
\(\Rightarrow\left(x+2019\right)\times\left(\frac{1}{1998}-\frac{1}{1994}+\frac{1}{652}-\frac{1}{648}\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x+2019=0\\\frac{1}{1998}-\frac{1}{1994}+\frac{1}{652}-\frac{1}{648}=0\end{cases}}\)
Vì \(\frac{1}{1998}-\frac{1}{1994}+\frac{1}{652}-\frac{1}{648}\ne0\)
\(\Rightarrow x+2019=0\)
\(\Rightarrow x=-2019\)
Vậy \(x=-2019\)
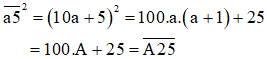
\(\frac{\left(135^{^2}\right)+130.135+65^2}{135^2-65^2}\)
=\(\frac{135^2+2.65.135+65^2}{\left(135-65\right).\left(135+65\right)}\)
=\(\frac{\left(135+65\right)^2}{70.200}\)
=\(\frac{200.200}{70.200}\)
=\(\frac{20}{7}\)
Học tốt
T cho mk nhé