NL
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
2
VN
Võ Ngọc Phương
VIP
1 tháng 8 2023
\(D=1+3+3^2+3^3+3^4+...+3^{2022}\)
\(3D=3.\left(1+3+3^2+3^3+3^4+...+3^{2022}\right)\)
\(3D=3+3^2+3^3+3^4+3^5+...+3^{2023}\)
\(3D-D=\left(3+3^2+3^3+3^4+3^5+...+3^{2023}\right)-\left(1+3+3^2+3^3+3^4+...+3^{2022}\right)\)
\(2D=\left(3^{2023}-1\right)\)
\(D=\left(3^{2023}-1\right):2\)
1 tháng 8 2023
3D=3+3^2+...+3^2023
=>2D=3^2023-1
=>\(D=\dfrac{3^{2023}-1}{2}\)
10 tháng 12 2023
\(2\cdot\left|-21\right|-3\cdot\left|125\right|-5\cdot\left|-33\right|-\left|2\cdot21\right|\)
\(=2\cdot21-3\cdot125-5\cdot33-2\cdot21\)
\(=-3\cdot125-5\cdot33=-375-165=-540\)
CM
23 tháng 2 2018
4 − 3 − 3 2 − 5 9 = 4 3 − 3 2 − 5 9 = − 1 6 − 5 9 = − 13 18 = 13 18
CM
12 tháng 7 2017
Cách 1: Tính giá trị từng biểu thức trong ngoặc
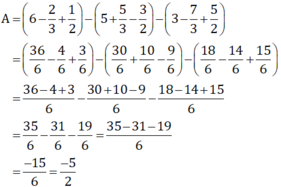
Cách 2: Bỏ dấu ngoặc rồi nhóm các số thích hợp
2 tháng 7 2023
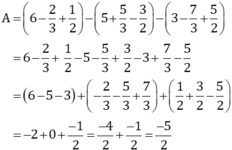
\(\dfrac{33-11\text{x}7}{12\text{x}11}=\dfrac{11\text{x}3-11\text{x}7}{12\text{x}11}\)
=\(\dfrac{11\text{x}\left(3-7\right)}{12\text{x}11}=\dfrac{11\text{x}\left(-4\right)}{12\text{x}11}\)
=\(\dfrac{-1}{3}\)
LD
3
28 tháng 8 2020
\(\frac{27^2.8^5}{6^6.32^3}=\frac{\left(3^3\right)^2.\left(2^3\right)^5}{2^3.3^3.\left(2^5\right)^3}=\frac{3^6.2^{15}}{2^3.3^3.2^{15}}=\frac{27}{8}\)
học tốt
11 tháng 9 2017
Bài 3 :
Vì \(\left(x-2\right)^2\ge0\forall x\)
Nên : \(A=\left(x-2\right)^2-4\ge-4\forall x\)
Vậy \(A_{min}=-4\) khi x = 2
S
11 tháng 9 2017
B1: lấy máy tính mà tính thôi bạn (nhớ lm theo từng bước)
B2:
a, \(\left|x-\frac{2}{3}\right|-\frac{1}{2}=\frac{5}{6}\)
\(\left|x-\frac{2}{3}\right|=\frac{4}{3}\)
\(\Rightarrow\orbr{\begin{cases}x-\frac{2}{3}=\frac{4}{3}\\x-\frac{2}{3}=\frac{-4}{3}\end{cases}\Rightarrow\orbr{\begin{cases}x=2\\x=\frac{-2}{3}\end{cases}}}\)
b, \(\frac{\left(-2\right)^x}{512}=-32\Rightarrow\left(-2\right)^x=-16384\Rightarrow x\in\varnothing\)
B3:
Vì \(\left(x-2\right)^2\ge0\Rightarrow A=\left(x-2\right)^2-4\ge-4\)
Dấu "=" xảy ra khi x = 2
Vậy GTNN của A = -4 khi x = 2
Nhân cả ba vế của S với 3 , ta được :
3S = 3.( 1 + 3 + 32 + 33 + .... + 32013 )
=> 3S = 3 + 32 + 33 + 34 + .... + 32014
Lấy biểu thức 3S - S , ta được :
3S S = ( 3 + 32 + 33 + 34 + .... + 32014 ) - ( 1 + 3 + 32 + 33 + .... + 32013 )
=> 2S = 32014 - 1
=> S = \(\frac{3^{2014}-1}{2}\)
S=1+3+3^2+3^3+...+3^2013
=>3S=3+3^2+3^3+3^4+....+3^2014
=>3S-S=(3+3^2+3^3+....+3^2014)-(1+3+3^2+3^3+...+3^2013)
=>2S=3^2014-1
=>S=(3^2014-1)/2