Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

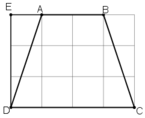
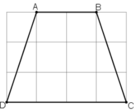
(Mỗi ô vuông là 1cm).
Nhìn vào hình vẽ ta thấy :
+ AB = 2cm
+ CD = 4cm.
+ Tính AD :
Xét tam giác vuông ADE có AE = 1cm, DE = 3cm.
⇒ AD2 = AE2 + DE2 (Định lý Pytago)
= 12 + 32 = 10
⇒ AD = √10 cm
+ Tính BC :
ABCD là hình thang cân nên BC = AD = √10 cm.
Vậy AB = 2cm, CD = 4cm, AD = BC = √10 cm.

Bài giải:
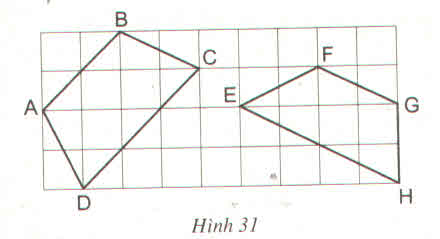
Để xét xem tứ giác nào là hình thang cân ta dùng tính chất
"Trong hình thang cân hai cạnh bên bằng nhau"
Tứ giác ABCD là hình thang cân vì có AD = BC.
Tứ giác EFGH không là hình thang cân vì EF > GH.
Để xét xem tứ giác nào là hình thang cân ta dùng tính chất
"Trong hình thang cân hai cạnh bên bằng nhau"
Tứ giác ABCD là hình thang cân vì có AD = BC.
Tứ giác EFGH không là hình thang cân vì EF > GH.

Xin lỗi bn mink mới học có lớp 5 thôi à nên MINK ko thể giúp bn, xin lỗi nha

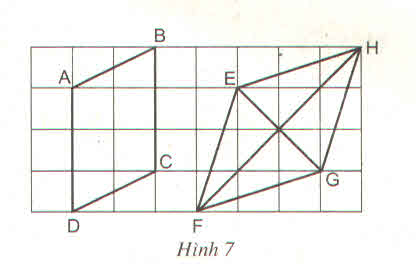
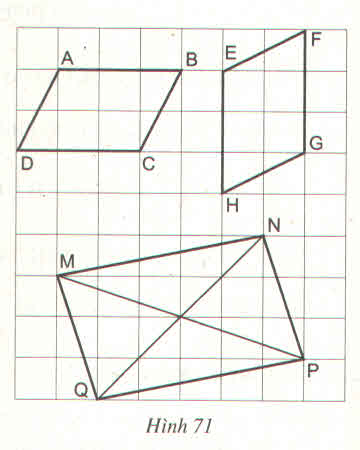
Cả ba tứ giác là hình bình hành.
- Tứ giác ABCD là hình bình hành vì có
AB // CD và AB = CD =3 (dấu hiệu nhận biết 3)
- Tứ giác EFGH là hình bình hành vì có
EH // FG và EH = FH = 3 (dấu hiệu nhận biết 3)
- Tứ giác MNPQ là hình bình hành vì có MN = QP và MQ = NP (dấu hiệu nhận biết 2)

Bài giải:
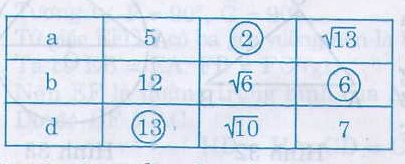
Cột thứ hai:
d2 = a2 + b2 = 52 + 122 = 25 + 144 = 169
Nên d = 13
Cột thứ ba:
a2 + b2 = d2 => a2 = d2 – b2=(√1010)2 - (√66)2
a2 = 10 – 6 = 4 => a = 2
Cột thứ tư:
a2 + b2 = d2 => b2 = d2 - a2 = 72 - (√1313)2
b2 = 49 – 13 = 36 => b = 6
Cột thứ hai:
d2 = a2 + b2 = 52 + 122 = 25 + 144 = 169
Nên d = 13
Cột thứ ba:
a2 + b2 = d2 => a2 = d2 – b2=(√1010)2 - (√66)2
a2 = 10 – 6 = 4 => a = 2
Cột thứ tư:
a2 + b2 = d2 => b2 = d2 - a2 = 72 - (√1313)2
b2 = 49 – 13 = 36 => b = 6

Bài giải:
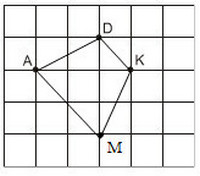
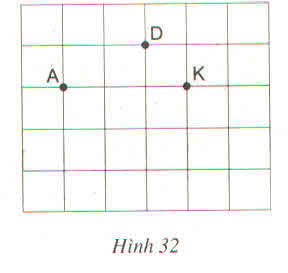
Có thể tìm được hai điểm M là giao điểm của các dòng kẻ sao cho nó cùng với ba điểm đã cho A, D, K là bốn đỉnh của một hình thang cân. Đó là hình thang AKDM1 (với AK là đáy) và hình thang ADKM2 (với DK là đáy).

\(AB^2 + AC^2 = 25^2 = 625\)
\(AD^2 + 81 = AB^2\)
\(AD^2 + 256 = AC^2\)
\(=> AD^2 + 81 + AD^2 + 256 = 625\)
=> \(2AD^2 = 288\)
=> \(AD^2 = 144\)
=> AD = 12(cm)
=>\( AB^2 = 9^2 + 12^2 = 225\)
=> AB = 15 (cm)
=> \(AC^2 = 12^2 + 16^2 = 400\)
=> AC = 20(cm)
và BC = 25(cm)

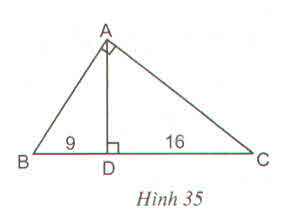
Ta có: \(BC=BD+DC=9+16=25\left(cm\right)\)
Xét \(\Delta DBA\) và \(\Delta ABC\):
\(\widehat{A}=\widehat{D}\left(=90^o\right)\)
\(\widehat{B}=\widehat{A_2}\)(cùng phụ với góc\(A_1\))
\(\Rightarrow\Delta DBA\)~\(\Delta ABC\)
\(\Rightarrow\dfrac{DB}{AB}=\dfrac{AB}{BC}\Leftrightarrow AB^2=DB.BC=9.25=225\Rightarrow AB=15\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC, có:
\(AB^2+AC^2=BC^2\Leftrightarrow15^2+AC^2=25^2\Rightarrow AC=\sqrt{25^2-15^2}=20\)
Vậy các cạnh của tam giác vuông ABC lần lượt là: \(15;20;25\)
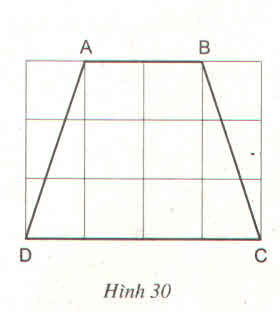


Bài giải:
Theo hình vẽ, ta có: AB = 2cm, CD = 4cm
Trong tam giác vuông AED, áp dụng định lý Pitago ta được:
AD2 = AE2 + ED2
= 32 + 12 =10
Suy ra AD = √1010cm
Vậy AB = 2cm, CD = 4cm, AD = BC = √1010cm
A B C H D
Áp dụng định lí Pitago :
\(AD^2 = AH^2 + DH^2\)
\(= 3^2 + 1^2\)
\(= 10\)
\(\Rightarrow AD=\sqrt{10}\)
Vậy \(AB = 2cm\);\(CD = 4cm\);\(AD=BC=\sqrt{10}\)