K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
Nguyễn Tuấn Tú
CTVHS
5 tháng 3 2023
Giải
Khoảng cách giữa hai số liền nhau là
7 - 2 = 12 - 7 = 17 - 12 = ... = 72 - 67 = 5
Số số hạng của dãy là:
(72 - 2) : 5 + 1 = 15 (số)
Tổng dãy là:
15 x (72 + 2) : 2 = 555
Đáp số:...
PT
2
12 tháng 12 2020
bn kia tính sai r kìa :vv
cách THCS:
\(\frac{2\times3\times6\times7}{2\times7\times18}=\frac{1\times1\times1\times1}{1\times1\times1}=1\)
AD
24 tháng 2 2021
a)\(8-\frac{3}{5}=\frac{40}{5}-\frac{3}{5}=\frac{37}{5}\)
b)\(\frac{24}{15}\times\frac{56}{72}\times\frac{10}{14}=\frac{13440}{15120}=\frac{8}{9}\)
c)\(\frac{32}{48}\times\frac{35}{21}\times\frac{63}{14}\times\frac{9}{30}=\frac{2}{3}\times\frac{5}{3}\times\frac{9}{2}\times\frac{3}{10}=\frac{270}{180}=\frac{3}{2}\)
d)\(7-\frac{72}{48}\times\frac{56}{60}-3=7-\frac{3}{2}\times\frac{14}{15}-3\)
\(=7-\frac{7}{5}-3\)
\(=\frac{35}{5}-\frac{7}{5}-\frac{15}{5}\)
\(=\frac{13}{5}\)
#H
(Sai thì sửa)
29 tháng 8 2023
a: \(A=\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}\right)^3+...+\left(\dfrac{1}{2}\right)^7\)
=>\(2\cdot A=1+\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2+...+\left(\dfrac{1}{2}\right)^6\)
=>\(2A-A=1-\left(\dfrac{1}{2}\right)^7=1-\dfrac{1}{128}=\dfrac{127}{128}\)
=>\(A=\dfrac{127}{128}\)
b: \(B=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{10\cdot11}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{10}-\dfrac{1}{11}\)
\(=1-\dfrac{1}{11}=\dfrac{10}{11}\)
PT
1
CM
10 tháng 8 2017
a. ….= 50 : 10 = 5
Hoặc…= 50 : 2 : 5 = 25 : 5 = 5
Hoặc…= 50 : 5 : 2 = 10 : 2 = 5
b. Kết quả: 1
c. Kết quả: 2
TN
1
19 tháng 4 2022
a. 2/5 + 3/7 + 3/5 + 4/7
= (2/5 + 3/5) + (3/7 + 4/7)
= 1 + 1 = 2
b. 2/3 x 4/9 + 2/3 x 5/9
= 2/3 x (4/9 + 5/9)
= 2/3 x 1 = 2/3
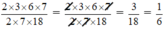
74/7
74/7