K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
.
CM
21 tháng 7 2018
Ta có (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
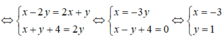
Vậy x = -3, y = 1.
Chọn đáp án D.
30 tháng 4 2016
Vì mình chưa học cao nên ko thể làm theo hàm số, đa thức được, thế này nhé:
a) (5x-2)-(x+6) = 0
=> 5x-2-x-6 = 0
=> (5x-x)-(2+6) = 0
=> (5-1)x-8 = 0
=> 4x =0 +8
=> 4x = 8
=> x = 8 : 4
=> x = 2
Vậy x = 2
b) (2x-3)-(3x+1)=4
=> 2x-3-3x-1 =4
=> (2x-3x)-(3+1) =4
=> (2-3) x - 4 = 4
=> 1x = 4+4
=> x = 8
Vậy x = 8
30 tháng 4 2016
a) (5x-2) - ( x+6)=0
=> 5x-2 = x+6
=> 5x - x = 6+2
=> 4x = 8
=> x=8:4=2
b) (2x-3)-(3x+1)=4
<=>2x - 3 - 3x - 1 = 4
<=> - x - 4 = 4
<=> -x = 4+4=8
<=>x=8
PT
1
NT
0
TA
27 tháng 6 2021
1, y' = \(\dfrac{m^2-9}{\left(3x-m\right)^2}\)
ycbt <=> \(\left\{{}\begin{matrix}m^2-9< 0\\\dfrac{m}{-3}\ne x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3< m< 3\\m\ge0\end{matrix}\right.\)
\(\Leftrightarrow0\le m\le3\)
TV
31 tháng 3 2017
A B C H D
Gọi H là chân đường cao từ C
Gọi D là trung điểm của BC \(D \in (d) \) với \((d)\) là đường trung trực của D
Do AB và CH vuông góc với nhau nên AH có vecto pháp tuyến \(\overrightarrow{n_{AB}}=\left(1,1\right)\) mà A(4,-2)
\(\Rightarrow\) Phương trình AB là:
\(x-4+y-(-2)=0 \Leftrightarrow x+y-2=0\)
Do \(B\in AB\) nên \(B(t,2-t)\ t\in \mathbb{R}\)
Do BC vuông góc với (d): 3x+4y-2=0 nên BC có vecto pháp tuyến \(\overrightarrow{n_{BC}}=\left(4,-3\right)\) mà B(t,2-t) thuộc BC
\(\Rightarrow\) Phương trình BC là:
\(4(x-t)-3(y-(2-t))=0 \Leftrightarrow 4x-3y+6-7t=0\)
\(\Rightarrow\) Tọa độ C là nghiệm của hệ:
\(\begin{cases} x-y+2=0\\4x-3y+6-7t=0 \end{cases} \Leftrightarrow \begin{cases} x=7t\\y=7t+2 \end{cases}\)
Do D là trung điểm BC nên tọa độ D là:\(D=(\dfrac{x_B+x_C}{2},\dfrac{y_B+y_C}{2})=(4t,3t+2)\)
Do \(D\in (d):3x+4y-2=0\) nên \(t=\dfrac{-1}{4}\)
\(\Rightarrow\) \(B\left(\dfrac{-1}{4},\dfrac{9}{4}\right),C\left(\dfrac{-7}{4},\dfrac{1}{4}\right)\)