Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ định nghĩa bằng nhau của hai số phức, ta có:
a) ⇔
;
b) ⇔
;
c) ⇔
⇔
.

a)3x+yi=(2y+1)(2−x)i⇔{3x=2y+1y=2−x⇔{x=1y=13x+yi=(2y+1)(2−x)i⇔{3x=2y+1y=2−x⇔{x=1y=1
b)2x+y−1=(x+2y−5)i⇔{2x+y−1=0x+2y−5=0⇔{x=−1y=3

\(2018^{2\left(x^2-y+1\right)}=\frac{2x+y}{x^2+2x+1}\)
\(\Leftrightarrow2\left(x^2-y+1\right)=log_{2018}\left(\frac{2x+y}{x^2+2x+1}\right)\)
\(\Leftrightarrow2\left(x^2+2x+1-2x-y\right)=log_{2018}\left(2x+y\right)-log_{2018}\left(x^2+2x+1\right)\)
\(\Leftrightarrow2\left(x^2+2x+1\right)+log_{2018}\left(x^2+2x+1\right)=log_{2018}\left(2x+y\right)+2\left(2x+y\right)\)
Đặt \(f\left(u\right)=log_{2018}u+2u\)
\(\begin{matrix}x^2+2x+1>0\\2x+y>0\end{matrix}\Rightarrow u>0\)
\(f'\left(u\right)=\frac{1}{u.ln2018}+2>0\)
Suy ra hàm số đồng biến
\(\Leftrightarrow f\left(x^2+2x+1\right)=f\left(2x+y\right)\)\(\Leftrightarrow x^2+2x+1=2x+y\) (tính chất hàm đồng biến)
\(\Leftrightarrow y=x^2+1\)
\(P=2y-3x=2x^2-3x+2\)
\(P=2\left(x-\frac{3}{4}\right)^2+\frac{7}{8}\)
\(P_{min}=\frac{7}{8}\) khi \(x=\frac{3}{4}\)
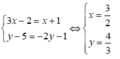




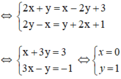
(3x – 2) + (2y – 1).i = (x + 1) – (y – 5).i