Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kéo dài đường cao AH lần lượt cắt BC và đường tròn ngoại tiếp tam giác ABC tại hai điển E và K, ta dễ dàng chứng minh được E là trung điểm HK
Đường cao \(AH\perp BC\) nên có phương trình \(x-y=0\), E là giao điểm của BC và AH \(\Rightarrow E\left(4;4\right)\) và H là trung điểm \(HK\Rightarrow K\left(3;3\right)\), suy ra bán kính đường tròn ngoại tiếp tam giác ABC là \(R=IK=\sqrt{5}\)
\(\Rightarrow\) phương trình đường tròn là \(\left(x-5\right)^2+\left(y-4\right)^2=5,\left(C\right)\)
Vậy hai điểm B, C là nghiệm của hệ hai phương trình đường thẳng BC và đường tròn (C) \(\Rightarrow B\left(3;5\right);C\left(6;2\right)\) và đỉnh A là nghiệm hệ của đường cao AH và đường tròn (C) \(\Rightarrow A\left(6;6\right)\)
Diện tích tam giác ABC là :
\(S_{ABC}=\frac{1}{2}d\left(A,BC\right).BC=\frac{1}{2}\frac{\left|6+6-8\right|}{\sqrt{2}}.3\sqrt{2}=6\)

Chọn C
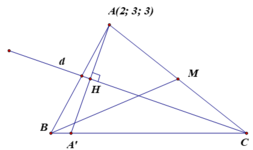
Gọi M là trung điểm của AC. Khi đó M thuộc vào đường trung tuyến kẻ từ B của tam giác ABC.
Giả sử M (3 – t ; 3 + 2t ; 2 – t) ∈ Δ suy ra C (4-2t; 3+4t; 1-2t).
Mà C thuộc và đường phân giác trong d của góc C nên ta có: 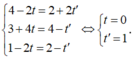
Suy ra C (4; 3; 1).
Gọi H là hình chiếu vuông góc của A trên đường phân giác trong d.
Suy ra H (2+2t';4-t';2-t') ![]()
Ta có ![]() ó 2. 2t'+ (-1) (1-t')+ (-1) (-1-t')=0 ó 4t'-1+t'+1+t'=0 ó t'=0
ó 2. 2t'+ (-1) (1-t')+ (-1) (-1-t')=0 ó 4t'-1+t'+1+t'=0 ó t'=0
=> H (2;4;2).
Gọi A' đối xứng với A qua đường phân giác trong d.
Suy ra A’ ∈ (BC) và A' (2;5;1). Khi đó ![]() là vectơ chỉ phương của đường thẳng BC.
là vectơ chỉ phương của đường thẳng BC.
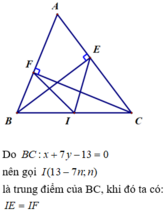

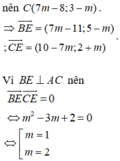
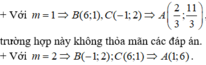


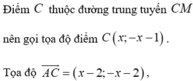

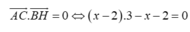
A B C H D
Gọi H là chân đường cao từ C
Gọi D là trung điểm của BC \(D \in (d) \) với \((d)\) là đường trung trực của D
Do AB và CH vuông góc với nhau nên AH có vecto pháp tuyến \(\overrightarrow{n_{AB}}=\left(1,1\right)\) mà A(4,-2)
\(\Rightarrow\) Phương trình AB là:
\(x-4+y-(-2)=0 \Leftrightarrow x+y-2=0\)
Do \(B\in AB\) nên \(B(t,2-t)\ t\in \mathbb{R}\)
Do BC vuông góc với (d): 3x+4y-2=0 nên BC có vecto pháp tuyến \(\overrightarrow{n_{BC}}=\left(4,-3\right)\) mà B(t,2-t) thuộc BC
\(\Rightarrow\) Phương trình BC là:
\(4(x-t)-3(y-(2-t))=0 \Leftrightarrow 4x-3y+6-7t=0\)
\(\Rightarrow\) Tọa độ C là nghiệm của hệ:
\(\begin{cases} x-y+2=0\\4x-3y+6-7t=0 \end{cases} \Leftrightarrow \begin{cases} x=7t\\y=7t+2 \end{cases}\)
Do D là trung điểm BC nên tọa độ D là:\(D=(\dfrac{x_B+x_C}{2},\dfrac{y_B+y_C}{2})=(4t,3t+2)\)
Do \(D\in (d):3x+4y-2=0\) nên \(t=\dfrac{-1}{4}\)
\(\Rightarrow\) \(B\left(\dfrac{-1}{4},\dfrac{9}{4}\right),C\left(\dfrac{-7}{4},\dfrac{1}{4}\right)\)