
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^2+6x+9=0\\ \Leftrightarrow x^2+2.3.x+3^2=0\\ \Leftrightarrow\left(x+3\right)^2=0\\ \Leftrightarrow x+3=0\\ \Leftrightarrow x=-3\)
Vậy \(x=-3\)

Biểu thức x x - 3 - x 2 + 3 x 2 x + 3 . x + 3 x 2 - 3 x - x x 2 - 9 xác định khi x – 3 ≠ 0,2x + 3 ≠ 0, x 2 - 3 x ≠ 0 và x 2 - 9 ≠ 0
Suy ra: x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ 3 và x ≠ ± 3
Với điều kiện x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3, ta có:
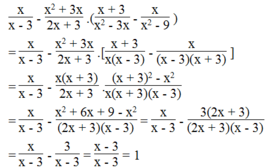
Vậy giá trị của biểu thức x x - 3 - x 2 + 3 x 2 x + 3 . x + 3 x 2 - 3 x - x x 2 - 9 bằng 1 khi x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3

1) \(\Leftrightarrow\left(x-4\right)\left(x+4\right)-x\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+4-x\right)=0\)
\(\Leftrightarrow\left(x-4\right)4=0\)
\(\Leftrightarrow x=4\)
2) \(\left(x+3\right)^2-\left(x-3\right)\left(x+5\right)=x^2+6x+9-x^2-2x+15=4x+24\)
3) \(2x^3+3x^2-2x+a=2x^2\left(x-2\right)+7x\left(x-2\right)+16\left(x-2\right)+32+a\)
Để \(2x^3+3x^2-2x+a⋮x-2\) thì \(32+a=0\Leftrightarrow a=-32\)
1.
x2 - 16 - x(x - 4) = 0
<=> (x2 - 42) - x(x - 4) = 0
<=> (x - 4)(x + 4) - x(x - 4) = 0
<=> (x + 4 - x)(x + 4) = 0
<=> 4(x + 4) = 0
<=> x + 4 = 0
<=> x = -4
2.
(x + 3)2 - (x - 3)(x + 5)
= x2 + 6x + 9 - (x2 + 5x - 3x - 15)
= x2 + 6x + 9 - x2 + 5x - 3x - 15
= x2 - x2 + 6x + 5x - 3x + 9 - 15
= 8x - 6

a: \(x^3-4x^2-x+4=0\)
=>\(\left(x^3-4x^2\right)-\left(x-4\right)=0\)
=>\(x^2\left(x-4\right)-\left(x-4\right)=0\)
=>\(\left(x-4\right)\left(x^2-1\right)=0\)
=>\(\left[{}\begin{matrix}x-4=0\\x^2-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x^2=1\end{matrix}\right.\Leftrightarrow x\in\left\{2;1;-1\right\}\)
b: Sửa đề: \(x^3+3x^2+3x+1=0\)
=>\(x^3+3\cdot x^2\cdot1+3\cdot x\cdot1^2+1^3=0\)
=>\(\left(x+1\right)^3=0\)
=>x+1=0
=>x=-1
c: \(x^3+3x^2-4x-12=0\)
=>\(\left(x^3+3x^2\right)-\left(4x+12\right)=0\)
=>\(x^2\cdot\left(x+3\right)-4\left(x+3\right)=0\)
=>\(\left(x+3\right)\left(x^2-4\right)=0\)
=>\(\left(x+3\right)\left(x-2\right)\left(x+2\right)=0\)
=>\(\left[{}\begin{matrix}x+3=0\\x-2=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\\x=-2\end{matrix}\right.\)
d: \(\left(x-2\right)^2-4x+8=0\)
=>\(\left(x-2\right)^2-\left(4x-8\right)=0\)
=>\(\left(x-2\right)^2-4\left(x-2\right)=0\)
=>\(\left(x-2\right)\left(x-2-4\right)=0\)
=>(x-2)(x-6)=0
=>\(\left[{}\begin{matrix}x-2=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=6\end{matrix}\right.\)

`x^3+4x^2+4x+3=0`
`<=>x^3+(x^2+3x^2)+(x+3x)+(1+3)=0`
`<=>(x^3+x^2+x)+(3x^2+3x+3)=0`
`<=>x(x^2+x+1)+3(x^2+x+1)=0`
`<=>(x+3)(x^2+x+1)=0`
`<=>x+3=0\ (x^2+x+1>0\ forall x)`
`<=>x=-3`
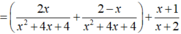
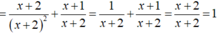
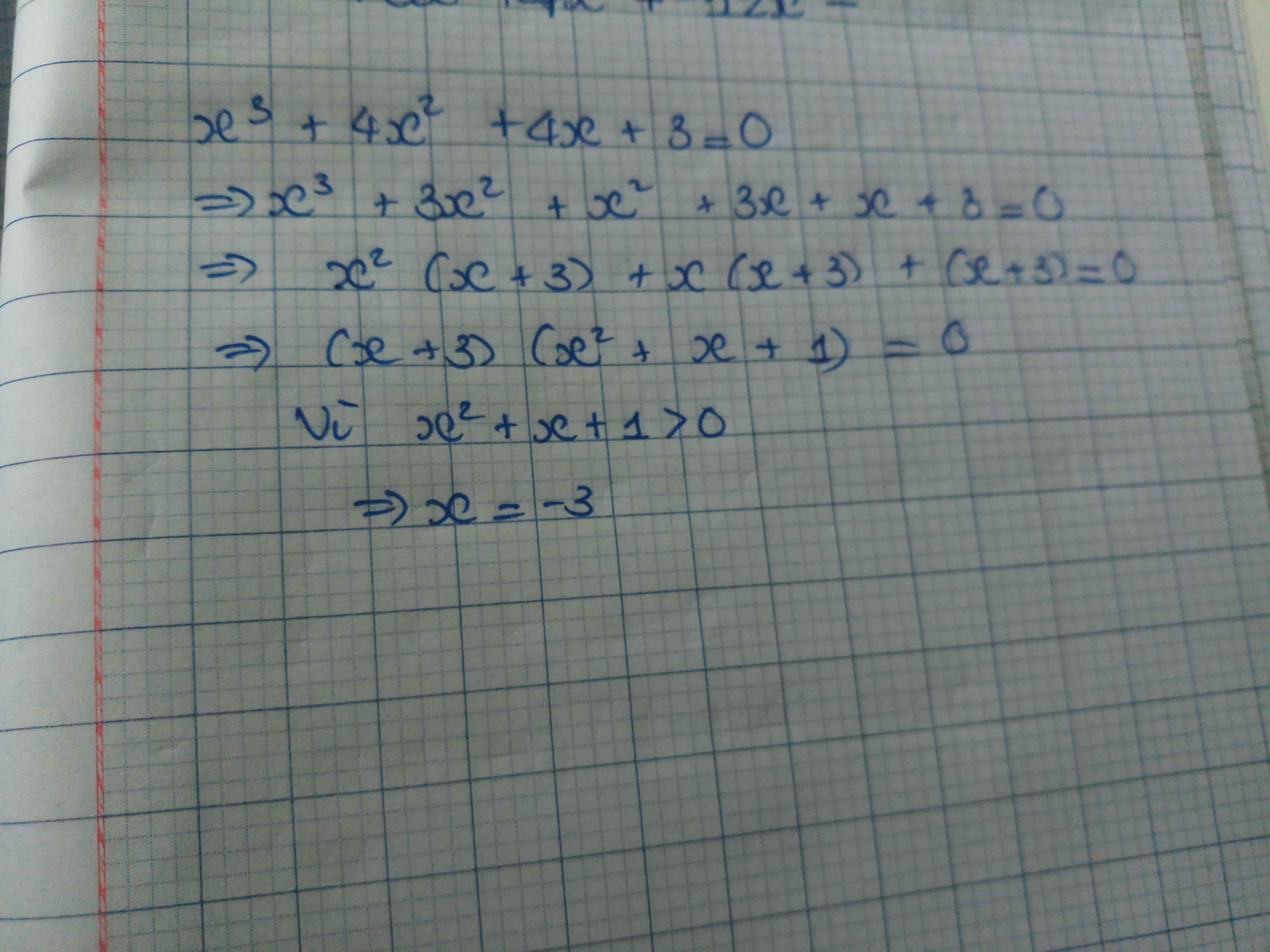
x2 - 4x + 3 = 0 <=> x2 - x - 3x + 3 = 0
<=> x( x - 1 ) - 3( x - 1 ) = 0
<=> ( x - 1 )( x - 3 ) = 0
<=> x = 1 hoặc x = 3
Trả lời:
\(x^2-4x+3=0\)
\(\Leftrightarrow x^2-3x-x+3=0\)
\(\Leftrightarrow\left(x^2-3x\right)-\left(x-3\right)=0\)
\(\Leftrightarrow x\left(x-3\right)-\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}}\)
Vậy x = 3; x = 1 là nghiệm của pt.