
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(T=\dfrac{3}{2}x^4-x^3+3x^2-\dfrac{1}{2}x+6+x^4+\dfrac{2}{3}x^3-2x^2-4x+1\)
\(=\dfrac{5}{2}x^4-\dfrac{1}{3}x^3+x^2-\dfrac{9}{2}x+7\)
b: \(T\left(2\right)=\dfrac{5}{2}\cdot16-\dfrac{1}{3}\cdot8+4-\dfrac{9}{2}\cdot2+7=\dfrac{118}{3}\)

a, \(A=x^2\left(2x-1\right)+x\left(x+8\right)=2x^3-x^2+x^2+8x=2x^3+8x\)
Thay x = -2, ta có:
\(2\cdot\left(-2\right)^3+8\cdot\left(-2\right)=-32\)
b, \(A=2x^3+8x=0\\ \Leftrightarrow2x\left(x^2+4\right)=0\\ \Leftrightarrow x=0\)
Vậy A=0 khi x=0
a,A = \(x^2\).( 2\(x\) - 1) + \(x\)(\(x+8\))
A = 2\(x^3\) - \(x^2\) + \(x^2\) + 8\(x\)
A = 2\(x^3\) + 8\(x\)
b, \(x=-2\) ⇒ A = 2.(-2)3 + 8.(-2) = - 32
A = 0 ⇔ 2\(x^3\) + 8\(x\) = 0
2\(x\left(x^2+4\right)\) = 0
vì \(x^2\) + 4 > 0 ∀ \(x\) ⇒ \(x\) =0

Do x,y tỉ lệ thuận nên k= \(\frac{{{y_1}}}{{{x_1}}} = \frac{{{y_2}}}{{{x_2}}} = \frac{{{y_1} + {y_2}}}{{{x_1} + {x_2}}} = \frac{{ - 20}}{{15}} = \frac{{ - 4}}{3}\)
\(\begin{gathered} \frac{{{y_1}}}{{{x_1}}} = \frac{{ - 4}}{3} \hfill \\ \frac{{{y_1}}}{{1,5}} = \frac{{ - 4}}{3} \hfill \\ {y_1} = \frac{{1,5 \times ( - 4)}}{3} \hfill \\ {y_1} = - 2 \hfill \\ \end{gathered} \)
Tương tự cho x=-10 bạn nhé.
Vì y tỉ lệ thuận với x nên y = k.x ( k khác 0). Ta có x1+x2=15 và y1+y2= -20
Mà y1= k.x1 và y2= k.x2 nên y1+y2= -20 hay k.x1+ k.x2 =-20; k. (x1+ .x2 )=-20 suy ra: k. 15 = -20
k = -20:15 = -4/3
Vậy hệ số tỉ lệ của y đối với x là -4/3
Vì k =-4/3 nên y = -4/3 . x
Thay x = 1,5 =3/2 vào y = -4/3 . x, ta được y = -4/3. 3/2= -2
Thay x = -10 vào y = -4/3 . x, ta được y = -4/3. (-10)= 40/3

a: x và y tỉ lệ thuận nên \(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_1+x_2}{y_1+y_2}=\dfrac{6}{-2}=-3\)
=>x=-3y
b: x=-3y
=>\(y=-\dfrac{1}{3}x\)
Thay x=2 vào \(y=-\dfrac{1}{3}x\), ta được:
\(y=-\dfrac{1}{3}\cdot2=-\dfrac{2}{3}\)
Thay x=4 vào \(y=-\dfrac{1}{3}x\), ta được:
\(y=-\dfrac{1}{3}\cdot4=-\dfrac{4}{3}\)

a: x và y là hai đại lượng tỉ lệ thuận
=>\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
mà \(x_1+x_2=2;y_1+y_2=10\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_1+x_2}{y_1+y_2}=\dfrac{2}{10}=\dfrac{1}{5}\)
=>\(\dfrac{x}{y}=\dfrac{1}{5}\)
=>y=5x
b: Khi x=1 thì \(y=5\cdot1=5\)

Vì x và y là hai đại lượng tỉ lệ thuận nên ta có:
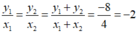
Vậy y tỉ lệ với x theo hệ số tỉ lệ là – 2 : y = -2x
Với x = -2 thì y = (-2). (-2) = 4
Chọn đáp án D
\(A=x^2-2x+2=2\Leftrightarrow x\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)