PV
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NM
1
NB
25 tháng 6 2021
Có\(\left|x-2010\right|+\left|x-2012\right|+\left|x-2014\right|\ge\left|x-2010+2014-x\right|+\left|x-2012\right|\ge2\)
mà\(\left|x-2010\right|+\left|x-2012\right|+\left|x-2014\right|=2\)
dấu "=' \(\Leftrightarrow\left\{{}\begin{matrix}x-2012=0\\2010\le x\le2014\end{matrix}\right.\)\(\Rightarrow x=2012\)
HT
2
KV
11 tháng 8 2023
\(\left(2x+1\right)\left(x^2-x\right)+x\left(5+x-2x^2\right)=3x+7\)
\(2x^3-2x^2+x^2-x+5x+x^2-2x^3=3x+7\)
\(5x-x=3x+7\)
\(4x-3x=7\)
\(x=7\)
11 tháng 8 2023
(2x+1)(x^2-x)+x(-2x^2+x+5)=3x+7
=>2x^3-2x^2+x^2-x-2x^3+x^2+5x=3x+7
=>-x^2-x+x^2+5x=3x+7
=>4x=3x+7
=>x=7
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
\(\dfrac{x}{y+z+1}\) = \(\dfrac{y}{x+z+2}\) = \(\dfrac{z}{x+y-3}\) = \(x+y+z\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{y+z+1}\)=\(\dfrac{y}{x+z+2}\)=\(\dfrac{z}{x+y-3}\)=\(\dfrac{x+y+z}{y+z+1+x+z+2+x+y-3}\)
\(x+y+z\) = \(\dfrac{x+y+z}{2.\left(x+y+z\right)}\) = \(\dfrac{1}{2}\) (1)
\(\dfrac{x}{y+z+1}\) = \(\dfrac{1}{2}\) ⇒ 2\(x\) = y+z+1
⇒ 2\(x\) + \(x\) = \(x+y+z+1\) (2)
Thay (1) vào (2) ta có: 2\(x\) + \(x\) = \(\dfrac{1}{2}\) + 1
3\(x\) = \(\dfrac{3}{2}\) ⇒ \(x=\dfrac{1}{2}\)
\(\dfrac{y}{x+z+2}\) = \(\dfrac{1}{2}\) ⇒ 2y = \(x+z+2\) ⇒ 2y+y = \(x+y+z+2\) (3)
Thay (1) vào (3) ta có: 2y + y = \(\dfrac{1}{2}\) + 2
3y = \(\dfrac{5}{2}\) ⇒ y = \(\dfrac{5}{6}\)
Thay \(x=\dfrac{1}{2};y=\dfrac{5}{6}\) vào (1) ta có: \(\dfrac{1}{2}+\dfrac{5}{6}+z\) = \(\dfrac{1}{2}\)
\(\dfrac{5}{6}\) + z = 0 ⇒ z = - \(\dfrac{5}{6}\)
Kết luận: (\(x;y;z\)) = (\(\dfrac{1}{2}\); \(\dfrac{5}{6}\); - \(\dfrac{5}{6}\))
16 tháng 8 2023
TH1: x + y + z 0
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
= = =
= = =
⇒ x + y + z =
⇒ x + y = - z
x + z = - y
y + z = - x
Thay y + z + 1 = - x + 1
⇒ =
⇒ 2x = - x + 1
⇒ 2x + x = + 1
⇒ 3x =
⇒ x =
Thay x + z + 2 = - y + 2
⇒ =
⇒ 2y = - y + 2
⇒ 2y + y = + 2
⇒ 3y =
⇒ y =
Thay x + y - 3 = - z - 3
⇒ \frac{1}{2}$
⇒ 2z = - z - 3
⇒ 2z + z = - 3
⇒ 3z =
⇒ z =
TH2: x + y + z = 0
⇒ = = = 0
⇒ x = y = z = 0
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 8 2023
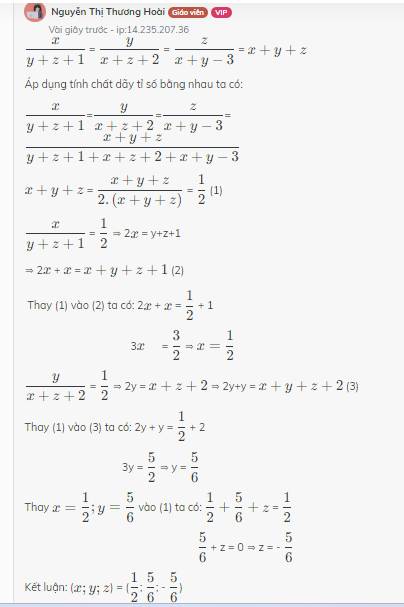
https://olm.vn/cau-hoi/tim-tat-ca-cac-so-xyz-biet-dfracxyz1dfracyxz2dfraczxy-3xyz-giair-chi-tiet-ho-e-vs-a.8297156371934
8 tháng 12 2016
x+2/327 + x+3/326 + x+4/325 + x+5/324 + x+349/5 = 0
=> x+2/327 + 1 + x+3/326 + 1 + x+4/325 + 1 + x+5/324 + 1 - x+349/5 - 4 = 0
=> x+329/327 + x+329/326 + x+329/325 + x+329/324 + x+329/5 = 0
=> (x+329).(1/327 + 1/326 + 1/325 + 1/324 + 1/5) = 0
Dễ thấy: 1/327 + 1/326 + 1/325 + 1/324 + 1/5 > 0
=> x + 329 = 0
=> x = -329
NT
1
TA
11 tháng 10 2017
\(\left(\frac{1}{7}x-\frac{2}{7}\right)\left(\frac{1}{5}x+\frac{3}{5}\right)\left(\frac{1}{3}x+\frac{4}{3}\right)=0\)
<=> \(\frac{x-2}{7}.\frac{x+3}{5}.\frac{x+4}{3}=0\)
<=> \(\frac{x-2}{7}=0\)hoặc \(\frac{x+3}{5}=0\); \(\frac{x+4}{3}=0\)
Nếu \(\frac{x-2}{7}=0\)<=> \(x-2=0\)<=> \(x=2\)
Nếu \(\frac{x+3}{5}=0\)<=> \(x+3=0\) <=> \(x=3\)
Nếu \(\frac{x+4}{3}=0\)<=> \(x+4=0\)<=> \(x=4\)
Vây x= 2 hoặc 3; 4
29 tháng 6 2019
\(a,\frac{1}{2}x+\frac{5}{2}=\frac{7}{2}x-\frac{3}{4}\)
\(\Leftrightarrow\frac{1}{2}x+\frac{5}{2}-\frac{7}{2}x=-\frac{3}{4}\)
\(\Leftrightarrow\frac{1}{2}x-\frac{7}{2}x+\frac{5}{2}=-\frac{3}{4}\)
\(\Leftrightarrow-3x+\frac{5}{2}=-\frac{3}{4}\)
\(\Leftrightarrow-3x=-\frac{13}{4}\)
\(\Leftrightarrow x=-\frac{13}{4}:(-3)=-\frac{13}{4}:\frac{-3}{1}=-\frac{13}{4}\cdot\frac{-1}{3}=\frac{13}{12}\)
29 tháng 6 2019
\(b,\frac{2}{3}x-\frac{2}{5}=\frac{1}{2}x-\frac{1}{3}\)
\(\Leftrightarrow\frac{2}{3}x-\frac{2}{5}-\frac{1}{2}x=-\frac{1}{3}\)
\(\Leftrightarrow\frac{2}{3}x-\frac{1}{2}x-\frac{2}{5}=-\frac{1}{3}\)
\(\Leftrightarrow\frac{1}{6}x-\frac{2}{5}=-\frac{1}{3}\)
\(\Leftrightarrow\frac{1}{6}x=\frac{1}{15}\)
\(\Leftrightarrow x=\frac{1}{15}:\frac{1}{6}=\frac{1}{15}\cdot6=\frac{6}{15}=\frac{2}{5}\)
\(c,\frac{1}{3}x+\frac{2}{5}(x+1)=0\)
\(\Leftrightarrow\frac{1}{3}x+\frac{2}{5}x+\frac{2}{5}=0\)
\(\Leftrightarrow\frac{11}{15}x=-\frac{2}{5}\)
\(\Leftrightarrow x=-\frac{6}{11}\)
d,e,f Tương tự
PT
1
15 tháng 3 2016
ta có: 5/x = 1/8 => x= 1/8 x 5 = 5/8
=> x= 8
duyệt đi