Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\frac{n+19}{n-2}=\frac{n-2+21}{n-2}=1+\frac{21}{n-2}\)
Để phân số tối giản thì: \(\frac{21}{n-2}\in Z\)
\(\Rightarrow21⋮n-2\)
\(\Rightarrow n-2\inƯ\left(21\right)=\left\{1;-1;3;-3;7;-7;21;-21\right\}\)
\(\Rightarrow n\in\left\{3;1;5;-1;9;-5;23;-19\right\}\)

\(M=\frac{5n+17}{4n+13}=\frac{4n+13+n+4}{4n+13}=1+\frac{n+4}{4n+13}\)
Để M đạt GTLN thì \(\frac{n+4}{4n+13}\)Đạt GTLN \(\Rightarrow4n+13\) đạt GTNN dương
Ta có : \(4n+13=1\)
\(\Leftrightarrow4n=-12\)\(\Rightarrow n=-3\)
Vậy M đạt GTLN = 2 khi n=-3

Đặt \(A=\frac{5a-17}{4a-23}=\frac{4.\left(5a-17\right)}{4.\left(4a-23\right)}=\frac{20a-68}{4.\left(4a-23\right)}=\frac{20a-115+47}{4.\left(4a-23\right)}=\frac{5.\left(4a-23\right)+47}{4.\left(4a-23\right)}\)
\(=>A=\frac{5.\left(4a-23\right)}{4.\left(4a-23\right)}+\frac{47}{4.\left(4a-23\right)}=\frac{5}{4}+\frac{47}{4.\left(4a-23\right)}=\frac{5}{4}+\frac{57}{16a-92}\)
Để A đạt giá trị lớn nhất
=>\(\frac{5}{4}+\frac{47}{16a-92}\)đạt giá trị lớn nhất
=>\(\frac{47}{16a-92}\)đạt giá trị lớn nhất
=>16a-92 đạt giá trị bé nhất
và 16a-92\(\ge1\)
=>16a\(\ge93\)>80
=>16a>80
=>a>5
Để 16a-92 đạt giá trị bé nhất
=>a đạt giá trị bé nhất
mà a là số tự nhiên
=>a=6
Khi đó: \(A=\frac{5}{4}+\frac{47}{16.6-92}=\frac{5}{4}+\frac{47}{4}=13\)
Vậy A đạt giá trị lớn nhất là 13 khi a=6

A=\(\frac{5a-17}{4a-23}=\frac{\frac{5}{4}.\left(4a-23\right)+\frac{115}{4}-17}{4a-23}=\frac{5}{4}+\frac{47}{4.\left(4a-23\right)}\)
Để A lớn nhất thì \(\frac{1}{4a-23}\) là số dương lớn nhất => 4a-23 là nhỏ nhất mà a là số tự nhiên=>4a-23=1 => a=6
Vậy a=6 thì A có giá trị lớn nhất là:\(\frac{5}{4}+\frac{47}{4}=\frac{52}{4}\)=\(13\)
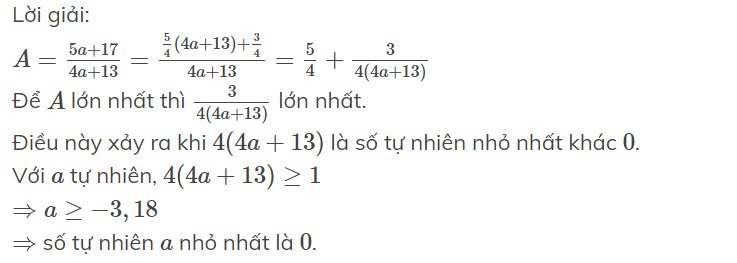
bạn có thể cho mình lời giải k