K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
1
25 tháng 3 2020
Ta có:
\(\left(2-4m\right)x+3m\cdot m-6m-9=0\)
\(\Leftrightarrow\left(2-4m\right)x+3m^2-6m-9=0\)
\(\Leftrightarrow\left(2-4m\right)x+3\left(m^2-2m+1\right)-12=0\)
\(\Leftrightarrow\left(2-4m\right)x=12-3\left(m-1\right)^2\)
Để phương trình sau có vô số nghiệm thì \(2-4m=0;12-3\left(m-1\right)^2=0\)
\(\Leftrightarrow m=\frac{1}{2};m=3;m=-1\)
Vậy.................
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
\(VT=\left|x-1\right|+\left|2-x\right|\ge\left|x-1+2-x\right|=1\)
\(VP=-4x^2+12x-9-1=-\left(2x-3\right)^2-1\le-1\)
\(\Rightarrow VT>VP\) ; \(\forall x\)
\(\Rightarrow\) Pt đã cho luôn luôn vô nghiệm
b.
\(\Leftrightarrow\left(m^2+3m\right)x=-m^2+4m+21\)
\(\Leftrightarrow m\left(m+3\right)x=\left(7-m\right)\left(m+3\right)\)
Để pt có nghiệm duy nhất \(\Rightarrow m\left(m+3\right)\ne0\Rightarrow m\ne\left\{0;-3\right\}\)
Khi đó ta có: \(x=\dfrac{\left(7-m\right)\left(m+3\right)}{m\left(m+3\right)}=\dfrac{7-m}{m}\)
Để nghiệm pt dương
\(\Leftrightarrow\dfrac{7-m}{m}>0\Leftrightarrow0< m< 7\)
NT
0
ML
2
7 tháng 3 2017
- PT Vô nghiệm khi 2m-1=0 và 3m-5 \(\ne\) 0( Vì một cái bằng 0 cộng một cái khác 0 mà kết quả bằng 0 thì quá vô lí )
- <=>m=1/2 và m \(\ne\) 5/3
- Vậy PT vô nghiệm khi m=1/2
:))
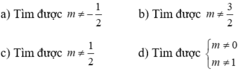
PT vô nghiệm khi 6mx = 0
<=> m = 0
PT vô nghiệm khi 6m = 0
<=> m = 0