K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TC
1
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 7 2021
\(y=\left|2sin^2x-sinx-1\right|-2sinx\)
Đặt \(sinx=t\in\left[-1;1\right]\)
\(\Rightarrow y=f\left(t\right)=\left|2t^2-t-1\right|-2t\)
BBT cho \(f\left(t\right)\) trên \(\left[-1;1\right]\):
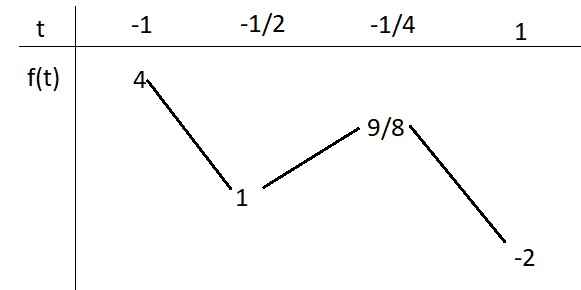
Từ BBT ta thấy \(y_{max}=4\) khi \(sinx=-1\); \(y_{min}=-2\) khi \(sinx=1\)
QN
1
HP
21 tháng 8 2021
Đặt \(sinx=t\left(t\in\left[-1;1\right]\right)\)
\(y=\left|sinx+cos2x\right|=\left|2sin^2x-sinx-1\right|\)
\(\Leftrightarrow y=\left|f\left(t\right)\right|=\left|2t^2-t-1\right|\)
\(f\left(-1\right)=2\Rightarrow y=2\)
\(f\left(1\right)=0\Rightarrow y=0\)
\(f\left(\dfrac{1}{4}\right)=-\dfrac{9}{8}\Rightarrow y=\dfrac{9}{8}\)
\(\Rightarrow y_{min}=0;y_{max}=2\)
NN
1
DD
Đoàn Đức Hà
Giáo viên
23 tháng 7 2021
\(y=\sqrt{3}cos2x+2sinxcosx-2\)
\(=\sqrt{3}cos2x+sin2x-2\)
Ta có: \(\left|\sqrt{3}cos2x+sin2x\right|\le\sqrt{\left(\sqrt{3}\right)^2+1^2}=2\)
Do đó \(-2\le\sqrt{3}cos2x+sin2x\le2\)
\(\Leftrightarrow-4\le\sqrt{3}cos2x+sin2x-2\le2\).
Ta có: \(\left|\sqrt{3}cosx-sinx\right|\le\sqrt{\left(\sqrt{3}\right)^2+\left(-1\right)^2}=2\)
Do đó \(-2\le\sqrt{3}cosx-sinx\le2\)
NH
1
HT
27 tháng 9 2020
\(y=1-2\sin^2x-\sin x+3=-2\sin^2x-\sin x+4\)
\(\sin x=t;t\in\left[-1;1\right]\)
Xét hàm f(t) trên [-1;1]
\(f\left(-1\right)=-2+1+4=3\)
\(f\left(1\right)=-2-1+4=1\)
\(f\left(-\frac{1}{4}\right)=-2.\frac{1}{16}+\frac{1}{4}+4=\frac{33}{8}\)
\(\Rightarrow\left\{{}\begin{matrix}y_{max}=\frac{33}{8};"="\Leftrightarrow\sin x=-\frac{1}{4}\Rightarrow x=...\\y_{min}=1;"="\Leftrightarrow\sin x=1\end{matrix}\right.\)
HP
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 9 2021
\(y=2\left(\dfrac{1}{2}sin2x+\dfrac{\sqrt{3}}{2}cos2x\right)=2sin\left(2x+\dfrac{\pi}{3}\right)\)
\(-1\le sin\left(2x+\dfrac{\pi}{3}\right)\le1\Rightarrow-2\le y\le2\)
\(y_{min}=-2\) khi \(sin\left(2x+\dfrac{\pi}{3}\right)=-1\Rightarrow x=-\dfrac{5\pi}{12}+k\pi\)
\(y_{max}=2\) khi \(sin\left(2x+\dfrac{\pi}{3}\right)=1\Rightarrow x=\dfrac{\pi}{12}+k\pi\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2020
a/ \(y=sin2x+\left(\sqrt{3}+1\right)cos2x+sin^2x-cos^2x-1\)
\(=sin2x+\sqrt{3}cos2x-1=2sin\left(2x+\frac{\pi}{3}\right)-1\)
Do \(-1\le sin\left(2x+\frac{\pi}{3}\right)\le1\Rightarrow-3\le y\le1\)
b/ \(y=2sin^2x-2cos^2x-3sinx.cosx-1\)
\(=-2cos2x-\frac{3}{2}sin2x-1=-\frac{5}{2}\left(\frac{3}{5}sinx+\frac{4}{5}cosx\right)-1\)
\(=-\frac{5}{2}sin\left(x+a\right)-1\Rightarrow-\frac{7}{2}\le y\le\frac{3}{2}\)
c/ \(y=1-sin2x+2cos2x+\frac{3}{2}sin2x=\frac{1}{2}sin2x+2cos2x+1\)
\(=\frac{\sqrt{17}}{2}\left(\frac{1}{\sqrt{17}}sin2x+\frac{4}{\sqrt{17}}cos2x\right)+1=\frac{\sqrt{17}}{2}sin\left(2x+a\right)+1\)
\(\Rightarrow-\frac{\sqrt{17}}{2}+1\le y\le\frac{\sqrt{17}}{2}+1\)
21 tháng 7 2020
Khi cho A td KOH thu được ancol đồng đẳng. => Các ancol là no đơn chức mạch hở.
Gọi CT các este: \(C_mH_{2m+1}COOC_{m'}H_{2m'+1};C_nH_{2n-1}COOC_{n'}H_{2n'-1};C_qH_{2q}\left(COOC_{q'}H_{2q'}\right)_2\)
TN2: Đốt hỗn hợp 3 muối.
Đặt \(n_{K_2CO_3}=x;n_{H_2O}=y\left(mol\right)\)
\(BTNT.K\Rightarrow n_{COOK^-}=2n_{K_2CO_3}=2x\left(mol\right)\\ BTNT.O\Rightarrow2n_{COOK^-}+2n_{O_2}=3n_{K_2CO_3}+2n_{CO_2}+n_{H_2O}\\ \Rightarrow x-y=0,3\\ BTKL\Rightarrow m_{M'}+m_{O_2}=m_{K_2CO_3}+m_{CO_2}+m_{H_2O}\\ \Rightarrow138x+18y=99,9\\ \Rightarrow\left\{{}\begin{matrix}x=0,675\\y=0,375\end{matrix}\right.\)
H2 muối gồm: \(C_mH_{2m+1}COOK\text{ }a\text{ }mol;C_nH_{2n-1}COOK\text{ }b\text{ }mol;C_qH_{2q}\left(COOK\right)_2\text{ }c\text{ }mol\)
\(\Rightarrow n_A=a+b+c=0,85\\ BTNT.C\Rightarrow\left(m+1\right)a+\left(n+1\right)b+\left(q+2\right)c=n_{K_2CO_3}+n_{CO_2}=1,75\\ \Rightarrow ma+nb+qc=0,4\\ BTNT.K\Rightarrow a+b+2c=1,35\\ BTNT.H\Rightarrow\left(2m+1\right)a+\left(2n-1\right)b+2qc=2n_{H_2O}=0,75\\ \Rightarrow a-b=-0,05\\ \Rightarrow\left\{{}\begin{matrix}a=0,15\\b=0,2\\c=0,5\end{matrix}\right.\\ \Rightarrow0,15m+0,2n+0,5q=0,4\)
Do \(m;q\ge0\Rightarrow n\le\frac{0,4}{0,2}=2\)
Mà \(n\ge2\Rightarrow n=2\Rightarrow m=q=0\)
13 tháng 7 2020
\(\text{c) }y=2sin^2x+4\sqrt{3}sinx\cdot cosx+6cos^2x+1\\ =\left(1-cos2x\right)+2\sqrt{3}sin2x+3\left(cos2x+1\right)+1\\ =2cos2x+2\sqrt{3}sin2x+5\)
Đặt \(t=2cos2x+2\sqrt{3}sin2x\)
\(\Rightarrow t^2\le\left[2^2+\left(2\sqrt{3}\right)^2\right]\left(cos^22x+sin^22x\right)=16\\ \Rightarrow-4\le t\le4\\ \Rightarrow1\le y\le9\\ \)
Vậy \(Min\text{ }y=1\Leftrightarrow sin2x=-\frac{1}{2}\)
\(Max\text{ }y=9\Leftrightarrow sin2x=\frac{1}{2}\)
NT
1
HP
10 tháng 9 2021
\(y=\sqrt{3}cosx-sinx=2\left(\dfrac{\sqrt{3}}{2}cosx-\dfrac{1}{2}sinx\right)=2cos\left(x+\dfrac{\pi}{6}\right)\)
Vì \(cos\left(x+\dfrac{\pi}{6}\right)\in\left[-1;1\right]\Rightarrow y=\sqrt{3}cosx-sinx\in\left[-2;2\right]\)
\(\Rightarrow y_{min}=-2\Leftrightarrow cos\left(x+\dfrac{\pi}{6}\right)=-1\Leftrightarrow x+\dfrac{\pi}{6}=\pi+k2\pi\Leftrightarrow x=\dfrac{5\pi}{6}+k2\pi\)
\(y_{max}=2\Leftrightarrow cos\left(x+\dfrac{\pi}{6}\right)=1\Leftrightarrow x+\dfrac{\pi}{6}=k2\pi\Leftrightarrow x=-\dfrac{\pi}{6}+k2\pi\)
\(y=\left|sinx-\left(1-2sin^2x\right)\right|=\left|2sin^2x+sinx-1\right|\)
Đặt \(t=sinx;-1\le t\le1\)
\(\Rightarrow y=\left|2t^2+t-1\right|\)
Đặt \(f\left(t\right)=2t^2+t-1;-1\le t\le1\)
Vẽ BBT của \(f\left(t\right)=2t^2+t-1;-1\le t\le1\) sẽ tìm được \(f\left(t\right)_{min}=-\dfrac{9}{8};f\left(t\right)_{max}=2\)
\(\Rightarrow0\le\left|f\left(t\right)\right|\le2\)
\(\Leftrightarrow0\le y\le2\)
\(\Rightarrow y_{min}=0\Leftrightarrow2sin^2x+sinx-1=0\Leftrightarrow\left[{}\begin{matrix}sinx=-1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(y_{max}=2\Leftrightarrow t=1\Leftrightarrow sinx=1\)