
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y=\left|2sin^2x-sinx-1\right|-2sinx\)
Đặt \(sinx=t\in\left[-1;1\right]\)
\(\Rightarrow y=f\left(t\right)=\left|2t^2-t-1\right|-2t\)
BBT cho \(f\left(t\right)\) trên \(\left[-1;1\right]\):
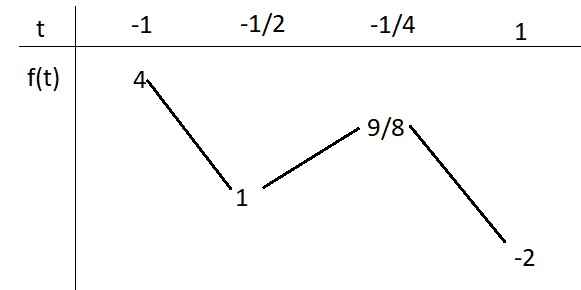
Từ BBT ta thấy \(y_{max}=4\) khi \(sinx=-1\); \(y_{min}=-2\) khi \(sinx=1\)

Đặt \(sinx=t\left(t\in\left[-1;1\right]\right)\)
\(y=\left|sinx+cos2x\right|=\left|2sin^2x-sinx-1\right|\)
\(\Leftrightarrow y=\left|f\left(t\right)\right|=\left|2t^2-t-1\right|\)
\(f\left(-1\right)=2\Rightarrow y=2\)
\(f\left(1\right)=0\Rightarrow y=0\)
\(f\left(\dfrac{1}{4}\right)=-\dfrac{9}{8}\Rightarrow y=\dfrac{9}{8}\)
\(\Rightarrow y_{min}=0;y_{max}=2\)

\(y=\sqrt{3}cos2x+2sinxcosx-2\)
\(=\sqrt{3}cos2x+sin2x-2\)
Ta có: \(\left|\sqrt{3}cos2x+sin2x\right|\le\sqrt{\left(\sqrt{3}\right)^2+1^2}=2\)
Do đó \(-2\le\sqrt{3}cos2x+sin2x\le2\)
\(\Leftrightarrow-4\le\sqrt{3}cos2x+sin2x-2\le2\).
Ta có: \(\left|\sqrt{3}cosx-sinx\right|\le\sqrt{\left(\sqrt{3}\right)^2+\left(-1\right)^2}=2\)
Do đó \(-2\le\sqrt{3}cosx-sinx\le2\)

\(y=sin^2x-6sinx+10\)
\(y=sin^2x-6sinx-7+17=\left(sinx+1\right)\left(sinx-7\right)+17\le17\)
\(y_{max}=17\) khi \(sinx=-1\)
\(y=sin^2x-6sinx+5+5=\left(1-sinx\right)\left(5-sinx\right)+5\ge5\)
\(y_{min}=5\) khi \(sinx=1\)
cái chỗ tìm ymax,min. X thuộc R x mình phải ngồi bấm từ giá trị để coi x nào là R hả, em thấy làm vậy hơi mất tg ko biết có tip nào nhanh hơn ko ạ

e/ Tử số đến đâu và mẫu số đến đâu bạn?
f/ Căn đến đâu bạn?
g/ Căn đến đâu bạn?
h/ \(y=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x\)
\(=1-\frac{1}{2}\left(2sinx.cosx\right)^2=1-\frac{1}{2}sin^22x\)
Do \(0\le sin^22x\le1\Rightarrow\frac{1}{2}\le y\le1\)
\(y_{max}=1\) khi \(sin^22x=0\)
\(y_{min}=\frac{1}{2}\) khi \(sin^22x=1\)
t/ \(y=\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)\)
\(y=1-3sin^2x.cos^2x=1-\frac{3}{4}\left(2sinx.cosx\right)^2\)
\(y=1-\frac{3}{4}sin^22x\)
Tượng tự câu trên \(\Rightarrow\frac{1}{4}\le y\le1\)
\(y_{min}=\frac{1}{4}\) khi \(sin^22x=1\)
\(y_{max}=1\) khi \(sin^22x=0\)
Tốt nhất là bạn sử dụng công cụ gõ công thức

2.
\(0\le\left|sinx\right|\le1\Rightarrow1\le y\le3\)
Min và max lần lượt là 3 và 1
3.
\(cos\left(x-\frac{\pi}{2}\right)\le1\Rightarrow y\le3.1+1=4\)
8.
\(y=\frac{1}{2}+\frac{1}{2}cos2x+2cos2x=\frac{1}{2}+\frac{5}{2}cos2x\le\frac{1}{2}+\frac{5}{2}.1=3\)
15.
Nó đi qua vô số điểm nên ko có 4 đáp án để chọn thì ko ai có thể trả lời câu này cho bạn cả
18.
\(y=\frac{sinx+2cosx+1}{sinx+cosx+2}\Leftrightarrow y.sinx+y.cosx+2y=sinx+2cosx+1\)
\(\Leftrightarrow\left(y-1\right)sinx+\left(y-2\right)cosx=1-2y\)
\(\left(y-1\right)^2+\left(y-2\right)^2\ge\left(1-2y\right)^2\)
\(\Leftrightarrow2y^2+2y-4\le0\Rightarrow-2\le y\le1\)
\(\Rightarrow y_{max}=1\)

8.
\(y=cos^2x+2\left(2cos^2x-1\right)=5cos^2x-2\)
Do \(0\le cos^2x\le1\Rightarrow-2\le y\le3\)
\(y_{min}=-2;y_{max}=3\)
10.
\(y=2-\left(cosx+1\right)^2\le2\)
\(y_{max}=2\)
14.
Hàm tuần hoàn với chu kì \(T=\pi\)

8.
\(y=\left(cosx+1\right)^2-1\ge-1\Rightarrow y_{min}=-1\)
\(y=\left(cosx-1\right)\left(cosx+3\right)+3\le3\Rightarrow y_{max}=3\)
10.
\(y=2-\left(cosx+1\right)^2\le2\Rightarrow y_{max}=2\)
14.
Hàm tuần hoàn với chu kì \(T=\pi\)
15.
Đáp án A đúng
20.
\(-1\le sin\left(\frac{x}{2}+\frac{\pi}{7}\right)\le1\Rightarrow-5\le y\le-1\)
\(y_{max}=-1\) ; \(y_{min}=-5\)
\(y=1-2\sin^2x-\sin x+3=-2\sin^2x-\sin x+4\)
\(\sin x=t;t\in\left[-1;1\right]\)
Xét hàm f(t) trên [-1;1]
\(f\left(-1\right)=-2+1+4=3\)
\(f\left(1\right)=-2-1+4=1\)
\(f\left(-\frac{1}{4}\right)=-2.\frac{1}{16}+\frac{1}{4}+4=\frac{33}{8}\)
\(\Rightarrow\left\{{}\begin{matrix}y_{max}=\frac{33}{8};"="\Leftrightarrow\sin x=-\frac{1}{4}\Rightarrow x=...\\y_{min}=1;"="\Leftrightarrow\sin x=1\end{matrix}\right.\)