TM
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 4 2016
Ta có: |a-x|+|b-x|+|x-c|+|x-d|>=|a-x+b-x+x-c+x-d|=|a+b-c-d|=|(a-c)+(b-d)|
mà a<c;b<d nên |(a-c)+(b-d)|=-(a-c)-(b-d)
Vậy GTNN của |a-x|+|b-x|+|x-c|+|x-d| là -(a-c)-(b-d)
CC
1
27 tháng 3 2016
Ta có:
\(f\left(x\right)=0\), do đó với mọi giá trị của x thì đa thức này bằng 0
Ta có:
\(f\left(1\right)=a.1^2+b.1+c=a+b+c=0\)
\(\Rightarrow a+b+c+3=0+3=3\)
Vậy \(a+b+c=3\)
CN
3
24 tháng 1 2016
a) ta có: (x-3,5)2 lớn hơn hoặc bằng 0
=> (x-3,5)2 +2 >= 2
=> GTNN của bt (x-3,5)2+2 là 2
khi x-3,5 =0
=> x= 3,5
b) ta có: (2x-3)4 lớn hơn hoặc bằng 0
=> (2x-3)4 -5 >= -5
=> GTNN của bt (2x-3)4 - 5 là -5
khi 2x-3 = 0
=> 2x= 3
=> x= 3/2
tick mk nhìu nhé 
TM
Cho đa thức : P(x) = 2 (x - 3)2 + 5
Chứng minh rằng : Đa thức đã cho không có nghiệm
P/S:help me vs!!!
1
11 tháng 4 2016
Ta có: với mọi x ta luôn được :(x-3)2 \(\ge\) 0
=> 2(x-3)2 \(\ge\) 0
=> 2(x-3)2 +5 \(\ge\) 5
Vậy đa thức P(x) = 2(x-3)2+5 vô nghiệm.
CC
2
7 tháng 3 2016
a) Để đẳng thức xảy ra thì: 101x\(\ge\)0=>x\(\ge\)0
Suy ra: \(x+\frac{1}{101}+x+\frac{2}{101}+....+x+\frac{100}{101}=101x\)
<=>\(100x+\frac{1+2+....+100}{101}=101x\)
<=>x=\(\frac{\frac{\left(1+100\right).100}{2}}{101}=50\)
29 tháng 4 2016
Câu 1.
A = {15;16;17;18;19} (0,25đ)
Câu 2.
a. 2.(72 – 2.32) – 60
= 2.(49 – 2.9) – 60 (0,25đ)
= 2.31 – 60 (0,25đ)
= 62 – 60 = 2 (0,25đ)
b. 27.63 + 27.37
= 27.(63 + 37) (0,25đ)
= 27.100 (0,25đ)
= 2700 (0,25đ)
c. l-7l + (-8) + l-11l + 2
= 7 + (-8) + 11 + 2 (0,5 đ)
= 12 (0,25đ)
d. 568 – 34 {5.l9 – ( 4-1)2l + 10}
= 568 – 34 {5.[9-9] + 10} (0,25đ)
= 568 – 34.10
= 568 – 340 (0,25đ)
= 228 (0,25đ)
Câu 3.
a)2x + 3 = 52 : 5
2x + 3 =5 (0,25đ)
2x = 5-3 (0,25đ)
2x =2 (0,25đ)
x=1 (0,25đ)
b)
105 – ( x + 7) = 27 : 25
105 – ( x + 7) = 22 (0,25đ)
105 – ( x + 7) = 4 (0,25đ)
x + 7 = 105 – 4 (0,25đ)
x + 7 = 101 (0,25đ)
x = 101 – 7 (0,25đ)
x = 94 (0,25đ)
Câu 4.
Gọi x (hs) là số học sinh lớp 6B phải tìm (30<x< 38, x)
Vì hs lớp 6B xếp 2, hàng, 4 hàng, 8 hàng đều vừa đủ nên x⋮2; x⋮4; x⋮8 hay x ∈ BC{2;4;8} (0,25đ)
Ta có: BCNN(2,4,8) = 8 (0,25đ)
⇒ BC(2,4,8) = B(8) ={0; 8; 16;24; 32; 40; …}
Mặt khác: 30<x< 38 (0,25đ)
Nên x = 32
Vậy số học sinh lớp 6B là 32 học sinh (0,25đ)
Câu 5.
Khi M nằm giữa và cách đều hai điểm A và B (0,5đ)
Vẽ được hình có điểm M là trung điểm của AB (0,5đ)
Câu 6.a)
0,25đ
Điểm A nằm giữa O và B (0,25đ)
Vì OA < OB ( 4 < 8 ) (0,25đ)
Ta có: AO + AB = OB
3 + AB = 6 (0,25đ)
AB = 6 -3 = 3 cm (0,25đ)
Vậy OA = AB = 3 cm (0,25đ)
b)
Vì A nằm giữa O, B và cách đều O và B ( OA = AB ) (0,25đ)
Nên A là trung điểm OB (0,25đ)
29 tháng 4 2016
Câu 1.
Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau. (1 điểm)
Ví dụ:
0,5 điểm
b) Muốn chia một phân số hay một số nguyên cho một phân số, ta nhân số bị chia với số nghịch đảo của số chia (1 điểm)
Ví dụ:
0,5 điểm
Câu 2. ( 2 điểm)
Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau (1 điểm)
Câu 3. ( 2 điểm) mỗi ý đúng 0,5 điểm
Câu 4.
0,5 điểm
Câu 5. ( 1 điểm)
Số học sinh nữ lớp 6A là: 20 . 3/10 = 6 (HS) (0,5 điểm)
Số học sinh nam lớp 6A là: 20 – 6 = 14 (HS) (0,5 điểm)
Câu 6. ( 1,5 điểm)
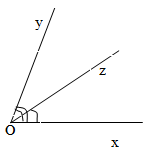
a) Vì ∠ xOz < ∠ xOy ( 350 <700) nên
tia Oz nằm giữa 2 tia Ox và Oy.
b) Vì tia Oz nằm giữa hai tia Ox và Oy nên
∠xOz + ∠zOy= ∠xOy hay 350 + ∠zOy = 700
=> ∠yOz = 350
c) Vì tia Oz nằm giữa hai tia Ox và Oy
và ∠xOz = ∠yOz = 350
nên Oz là tia phân giác của góc xOy
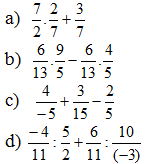
Ta có:
\(A=\left|x-4\right|+\left|x-2020\right|=\left|x-4\right|+\left|2020-x\right|\ge x-4+2020-x=2016\)
Dấu "=" xảy ra <=> x - 4 \(\ge0\)
và 2020 - x \(\ge0\)
<=> \(x\ge4\) và \(x\le2020\)
\(\Leftrightarrow4\le x\le2020\)
Vậy A đạt GTNN là 2016 \(\Leftrightarrow4\le x\le2020\)
7< y : 4 < 9