K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 1 2021
a) Ta có: \(Q=-x^2-y^2+4x-4y+2=-\left(x^2+y^2-4x+4y-2\right)\)
\(=-\left(x^2-4x+4+y^2+4y+4\right)+10\)
\(=-\left[\left(x-2\right)^2+\left(y+2\right)^2\right]+10\le10\forall x,y\)
Vậy MaxQ=10 khi x=2, y=-2
b) +Ta có: \(A=-x^2-6x+5=-\left(x^2+6x-5\right)=-\left(x^2+6x+9-14\right)\)
\(=-\left(x^2+6x+9\right)+14=-\left(x+3\right)^2+14\le14\forall x\)
Vậy MaxA=14 khi x=-3
+Ta có: \(B=-4x^2-9y^2-4x+6y+3=-\left(4x^2+9y^2+4x-6y-3\right)\)
\(=-\left(4x^2+4x+1+9y^2-6y+1-5\right)\)
\(=-\left[\left(2x+1\right)^2+\left(3y-1\right)^2\right]+5\le5\forall x,y\)
Vậy MaxB=5 khi x=-1/2, y=1/3
c) Ta có: \(P=x^2+y^2-2x+6y+12=x^2-2x+1+y^2+6y+9+2\)
\(=\left(x-1\right)^2+\left(y+3\right)^2+2\ge2\forall x,y\)
Vậy MinP=2 khi x=1, y=-3
S
12 tháng 7 2018
1/
a, \(A=4x^2-4x+5=4x^2-4x+1+4=\left(2x-1\right)^2+4\ge4\)
Dấu "=" xảy ra khi x=1/2
Vậy Amin=4 khi x=1/2
b, \(B=3x^2+6x-1=3\left(x^2+2x+1\right)-4=3\left(x+1\right)^2-4\ge-4\)
Dấu "=" xảy ra khi x=-1
Vậy Bmin = -4 khi x=-1
2/
a, \(A=10+6x-x^2=-\left(x^2-6x+9\right)+19=-\left(x-3\right)^2+19\le19\)
Dấu "=" xảy ra khi x=3
Vậy Amax = 19 khi x=3
b, \(B=7-5x-2x^2=-2\left(x^2-\frac{5}{2}x+\frac{25}{16}\right)+\frac{31}{8}=-2\left(x-\frac{5}{4}\right)^2+\frac{31}{8}\le\frac{31}{8}\)
Dấu "=" xảy ra khi x=5/4
Vậy Bmax = 31/8 khi x=5/4
10 tháng 9 2020
\(A=x^2-6x+10=\left(x-3\right)^2+1\ge1\)
\(\Rightarrow A_{min}=1\Leftrightarrow x=3\)
\(B=4x^2-4x+25=\left(2x-1\right)^2+24\ge24\)
\(\Rightarrow B_{min}=24\Leftrightarrow x=\frac{1}{2}\)
\(C=3x^2+9x+12=3\left(x+\frac{3}{2}\right)^2+\frac{21}{4}\ge\frac{21}{4}\)
\(\Rightarrow C_{min}=\frac{21}{4}\Leftrightarrow x=\frac{-3}{2}\)
1 tháng 8 2015
1. x2-8x+1 = x2 -2x.4 + 42 - 42 +1 = ( x- 4 )2 - 15
mà ( x - 4 )2 > 0
=> ( x - 4 )2 -15 > 0
Vậy -15 là gt min của biểu thức khi x = 4
2. x2 - 4x + y2 - 6y + 2 = x2 - 2.2x + 22 + y2 - 2.3y + 32 -11 = (x-2)2 + ( y - 3)2 -11
mà ( x - 2)2 > 0
( y - 3)2 > 0
Vậy -11 là gt min của biểu thức khi x=2 và y = 3
Mình nghĩ là bài 3 là tìm gt lớn nhất chứ bạn ^^
MN
3
TN
22 tháng 6 2018
A \(=x^2+6x+5\)
\(=x^2+6x+9-4\)
\(=\) \(\left(x+3\right)^2-4\)\(< =-4\)
dấu bằng xảy ra <=> \(\left(x+3\right)^2=0\)
<=>\(x=-3\)
B= \(x^2-4x-3\)
\(=x^2-4x+4-7\)
\(=\left(x-2\right)^2-7< =-7\)
dấu bằng xảy ra <=> \(\left(x-2\right)^2=0\)
<=> \(x=2\)
22 tháng 6 2018
P/s pain sẽ mẫu cho 1 bài nha bài còn lại bạn tự làm :)
\(A=x^2+6x+5\)
\(A=x^2+6x+9-4\)
\(A=\left(x+3\right)^2-4\ge-4\)
\(\Rightarrow A_{min}=-4\)
dấu "=" xảy ra \(\Leftrightarrow x+3=0\Leftrightarrow x=-3\)
Vậy Amin = -4 khi x = -3
O
1
9 tháng 1 2018
\(A=\frac{x^2}{2}-\frac{x}{6}+3\)
\(2A=x^2-\frac{x}{3}+6=x^2-2.x\frac{1}{6}+\frac{1}{36}+\frac{35}{36}\)
\(2A=\left(x+\frac{1}{6}\right)^2+\frac{35}{36}\ge\frac{35}{36}\)
\(\Rightarrow A\ge\frac{35}{72}\)Dấu "=" xảy ra khi \(x=\frac{-1}{6}\)
b)\(B=x^4-4x^3+6x^2-4x+5\)
\(B=\left(x^4-4x^3+4x^2\right)+\left(2x^2-4x+2\right)+3\)
\(B=\left(x^2-2x\right)^2+2\left(x+1\right)^2+3\ge3\)
Dấu "=" xảy ra khi:\(x=0;-1;2\)
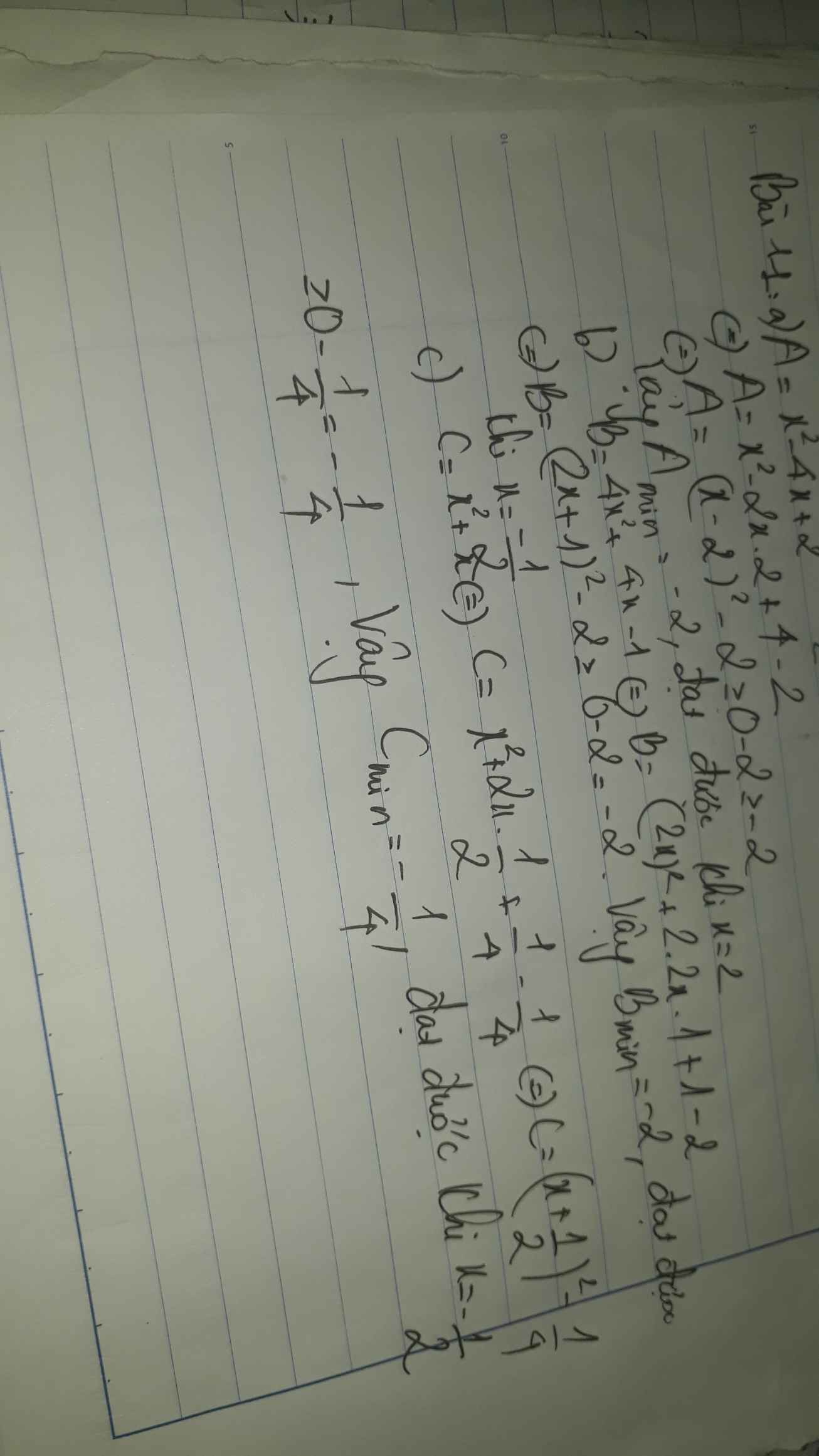
http://123link.pro/cS4uABOY
B = 5 - 4x2 + 6x
= -(4x2 - 6x - 5)
= -(4x2 - 6x + 9/4 - 29/4)
= -(4x2 - 6x + 9/4) + 29/4
B = -(2x - 3/2)2 + 29/4
Vì -(2x - 3/2)2 \(\le0\forall x\)
Nên : B = -(2x - 3/2)2 + 29/4 \(\le\frac{29}{4}\forall x\)
Vậy Bmax = \(\frac{29}{4}\) khi x = \(\frac{3}{4}\)