K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
1 tháng 4 2018
a) * Nếu M ≥ a ⇔ 1 M ≤ 1 a ;
* Nếu M ≤ a ⇔ 1 M ≥ 1 a ;
b) Ta có x 2 - 4x + 12 = ( x - 2 ) 2 + 8 ≥ 8 hay 1 x 2 + 2 x + 11 ≤ 1 10 ⇒ N ≥ − 1 2
Giá trị nhỏ nhất của N = − 1 2 khi x = -1.
GN
2
21 tháng 7 2017
x^2-4x+7=(x^2-4x+4)+3=(x-2)^2+3>3
=> min=3<=>(x-2)^2=0
<=>x=2
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2023
\(N=\dfrac{-5}{x^2-4x+7}=\dfrac{-5}{\left(x-2\right)^2+3}\ge-\dfrac{5}{3}\)
\(N_{min}=-\dfrac{5}{3}\) khi \(x=2\)
TG
23 tháng 6 2021
a)
\(A=4x-x^2+3=-\left(x^2-4x-3\right)=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\)
Daaus = xayr ra khi: x = 2
b) \(B=4x^2-12x+15=4\left(x^2-3x+9\right)-21=4\left(x-3\right)^2-21\ge-21\)
Dấu = xảy ra khi x = 3
c) \(C=4x^2+2y^2-4xy-4y+1=\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3=\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)
Dấu = xảy ra khi
2x = y và y = 2
=> x = 1 và y = 2
23 tháng 6 2021
a) A = \(-x^2+4x+3=-\left(x-2\right)^2+7\le7\)
Dấu "=" <=> x = 2
b) \(4x^2-12x+15=\left(2x-3\right)^2+6\ge6\)
Dấu "=" xảy ra <=> \(x=\dfrac{3}{2}\)
c) \(4x^2+2y^2-4xy-4y+1\)
= \(\left(4x^2-4xy+y^2\right)+\left(y^2-4y+4\right)-3\)
= \(\left(2x-y\right)^2+\left(y-2\right)^2-3\ge-3\)
Dấu "=" <=> \(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
OD
8 tháng 7 2017
Vì 7 không đổi nên 3x2 + 4x + 7\(\ge\)7
3x2 + 4x = 0
x ( 3x + 4) =0
x =0, x =\(\frac{-4}{3}\)
GTNN = 7
10 tháng 7 2017
Ta có : 3x2 + 4x + 7
= 2x2 + (x2 + 4x + 4) + 3
= 2x2 + (x + 2)2 + 3
Mà : 2x2 \(\ge0\forall x\)
10 tháng 7 2017
Đặt
\(A=3x^2+4x+7\)
=> \(A=3\left(x+\frac{2}{3}\right)^2+\frac{17}{3}\)
=> \(Min_A=\frac{17}{3}\Leftrightarrow x=-\frac{2}{3}\)
7 tháng 11 2021
\(A=\left(x-1\right)^2+8\ge8\\ A_{min}=8\Leftrightarrow x=1\\ B=\left(x+3\right)^2-12\ge-12\\ B_{min}=-12\Leftrightarrow x=-3\\ C=x^2-4x+3+9=\left(x-2\right)^2+8\ge8\\ C_{min}=8\Leftrightarrow x=2\\ E=-\left(x+2\right)^2+11\le11\\ E_{max}=11\Leftrightarrow x=-2\\ F=9-4x^2\le9\\ F_{max}=9\Leftrightarrow x=0\)
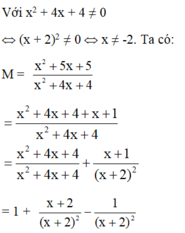
tìm giá trị nhỏ nhất: 5x2-4x+7
5x2-4x+7=5(x2-4/5.x+7/5)
\(=\left[\left(x-\frac{2}{5}\right)^2+\frac{31}{25}\right].5\)
\(=5\left(x-\frac{2}{5}\right)^2+\frac{31}{5}\ge\frac{31}{5}\forall x\)
Dấu = xảy ra khi x=2/5
vậy...