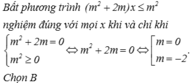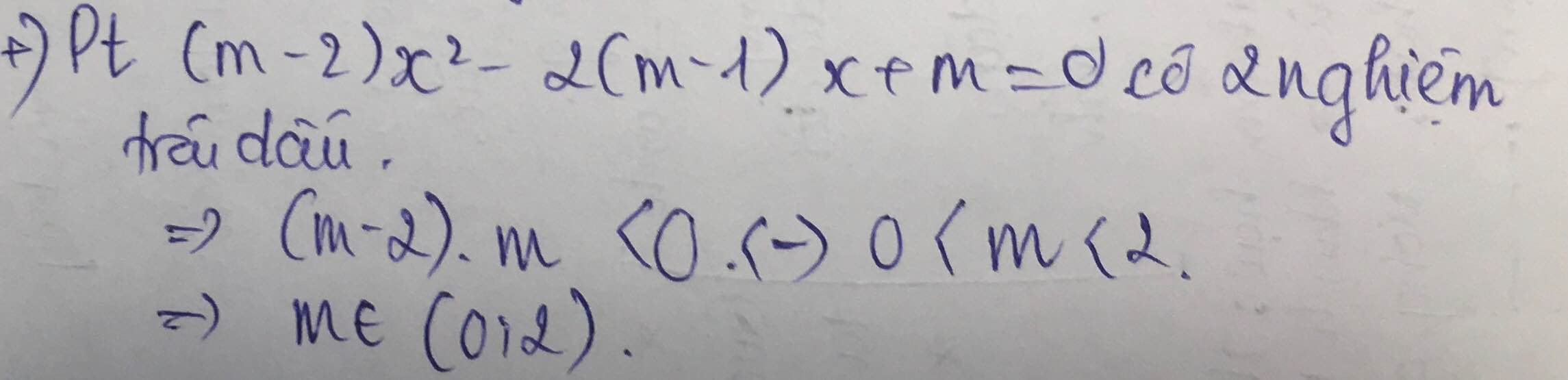Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^2+2mx-2m+3>=0\)(1)
\(\text{Δ}=\left(2m\right)^2-4\cdot1\cdot\left(-2m+3\right)\)
\(=4m^2+8m-12\)
\(=4\left(m^2+2m-3\right)=4\left(m+3\right)\left(m-1\right)\)
Để bất phương trình (1) đúng với mọi x thuộc R thì \(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4\left(m+3\right)\left(m-1\right)< =0\\1>0\end{matrix}\right.\)
=>\(\left(m+3\right)\left(m-1\right)< =0\)
TH1: \(\left\{{}\begin{matrix}m+3>0\\m-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-3\\m< 1\end{matrix}\right.\)
=>-3<m<1
TH2: \(\left\{{}\begin{matrix}m+3< 0\\m-1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< -3\\m>1\end{matrix}\right.\)
=>\(m\in\varnothing\)

Để phương trình có nghiệm đúng với mọi x thì
(2m)^2-4(m-2)(-m-2)<0 và m-2<0
=>4m^2+4(m^2-4)<0 và m<2
=>8m^2-16<0 và m<2
=>m^2<2
=>-căn 2<m<căn 2

+ Nếu m = 0 thì bất phương trình nghiệm đúng với mọi x;
+ Nếu m = -2 thì bất phương tình trở thành – 4x + 2 > 0, không nghiệm đúng với mọi x.
+ Nếu m ≠ 0 và m ≠ -2 thì bất phương trình nghiệm đúng với mọi x khi và chỉ khi
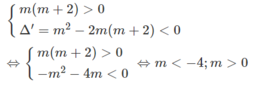
Đáp số: m < -4; m ≥ 0

2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=4m^2-4\left(m+2\right)\left(m-1\right)\ge0\\x_1x_2=\dfrac{m+2}{m-1}< 0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}-4m+8\ge0\\-2< m< 1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ge2\\-2< m< 1\end{matrix}\right.\Leftrightarrow m\in\varnothing\)

Để phương trình x 2 - 2 m x + m + 2 = 0 có hai nghiệm dương phân biệt
⇔ Δ ' > 0 S > 0 P > 0 ⇔ − m 2 − 1. m + 2 > 0 2 m > 0 m + 2 > 0 ⇔ m 2 − m − 2 > 0 m > 0 m > − 2 ⇔ m < − 1 , m > 2 m > 0 m > − 2
Vậy: m > 2
Đáp án cần chọn là: A