QT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 9 2023
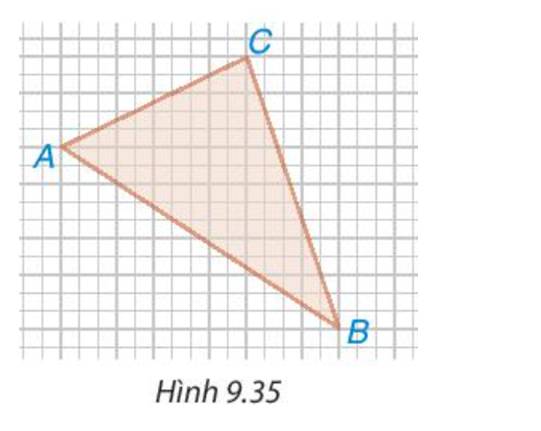
\(AC^2=100+25=125\Rightarrow AC=5\sqrt[]{5}\left(cm\right)\)
\(AB^2=100+225=325\Rightarrow AB=5\sqrt[]{13}\left(cm\right)\)
\(BC^2=225+25=250\Rightarrow BC=5\sqrt[]{10}\left(cm\right)\)
QT
1
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
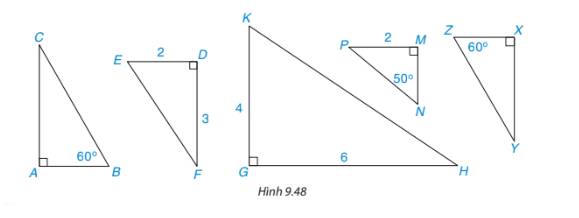
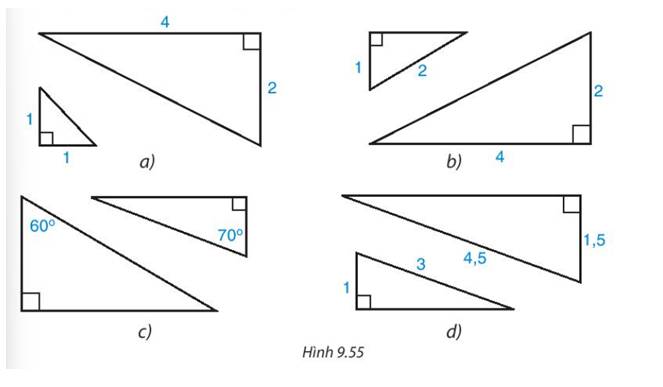
Các cặp tam giác vuông đồng dạng:
\(\begin{array}{l}\Delta ABC \backsim \Delta X{\rm{Z}}Y(\widehat A = \widehat X;\widehat B = \widehat Z)\\\Delta E{\rm{D}}F \backsim \Delta KGH\left( {\frac{{E{\rm{D}}}}{{KG}} = \frac{{DF}}{{GF}};\widehat {E{\rm{D}}F} = \widehat {KGH}} \right)\end{array}\)
QT
1
HQ
Hà Quang Minh
Giáo viên
13 tháng 1 2024
Cặp tam giác vuông ở hình d. Vì cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia
HQ
Hà Quang Minh
Giáo viên
13 tháng 1 2024
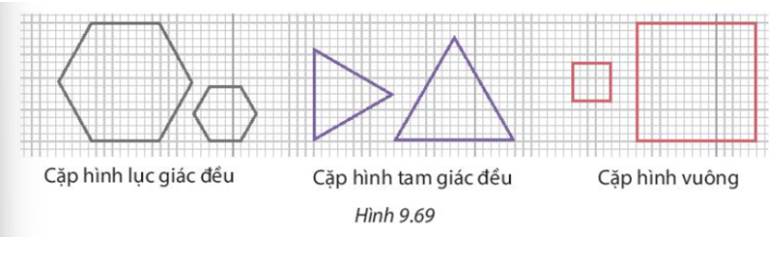
Cặp hình lục giác đều và cặp hình vuông là đồng dạng phối cảnh
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
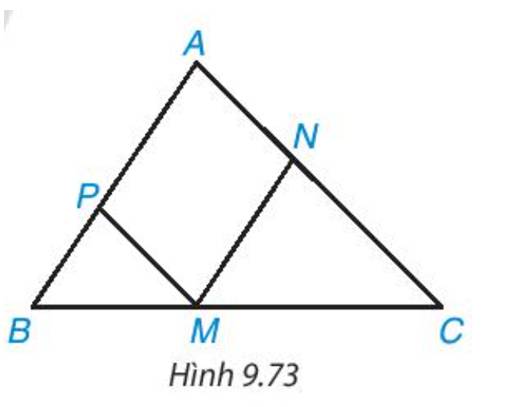
- ΔCNM ~ ΔCAB (vì MN // AB) (1)
- ΔMPB ~ ΔCAB (vì MP // AC) (2)
- Từ (1) và (2) => ΔCNM ~ ΔMPB
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
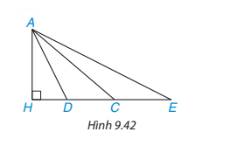
Áp dụng định lí Pythagore trong tam giác AHD vuông tại H có: \(A{{\rm{D}}^2} = A{H^2} + H{{\rm{D}}^2}\) (1)
Áp dụng định lí Pythagore trong tam giác AHC vuông tại H có: \(A{C^2} = A{H^2} + H{C^2}\) (2)
Áp dụng định lí Pythagore trong tam giác AHE vuông tại H có: \(A{E^2} = A{H^2} + H{E^2}\) (3)
Vì HE > HC > HD suy ra \(H{E^2} > H{C^2} > H{{\rm{D}}^2}\)(4)
Từ (1), (2), (3), (4) suy ra: \(A{{\rm{E}}^2} > A{C^2} > A{{\rm{D}}^2} \Rightarrow A{\rm{E}} > AC > A{\rm{D}}\)
Vậy đoạn AE là lớn nhất, đoạn AD là nhỏ nhất.
HQ
Hà Quang Minh
Giáo viên
10 tháng 9 2023
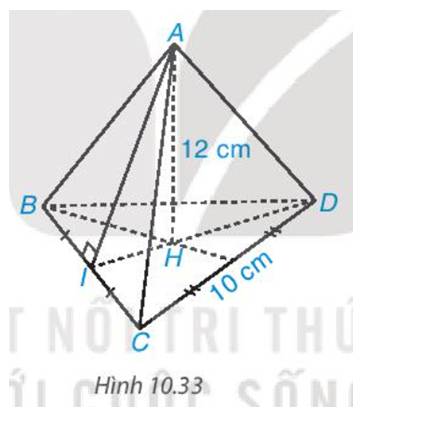
- Xét tam giác BID vuông tại I, có
\(I{{\rm{D}}^2} = B{{\rm{D}}^2} - B{I^2} = {10^2} - {5^2}\)
=> ID ≈ 8,66 (cm)
- Diện tích tam giác BCD là:
\({S_{BC{\rm{D}}}} = \frac{1}{2}.I{\rm{D}}.BC = \frac{1}{2}.8,66.10 = 43,3\left( {c{m^2}} \right)\)
- Thể tích hình chóp là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.43,3.12 \approx 173,2(c{m^3})\)
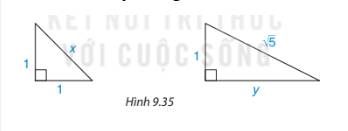
\(x^2=1^2+1^2\left(pythagore\right)\\ \Rightarrow x=\sqrt{2}\\ \sqrt{5}^2=1^2+y^2\left(pythagore\right)\\ \Rightarrow y=\sqrt{4}=2\)
a) \(x^2=1^2+1^2=2\Rightarrow x=\sqrt[]{2}\)
b) \(\left(\sqrt[]{5}\right)^2=y^2+1^2\Rightarrow y^2=5-1=4\Rightarrow y=2\)