K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
9 tháng 11 2017
TXĐ: R
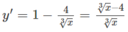
y′ = 0 ⇔ x = 64
Bảng biến thiên:
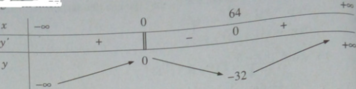
Vậy ta có y CD = y(0) = 0 và y CT = y(64) = -32.
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
Xét trên các miền xác định của các hàm (bạn tự tìm miền xác định)
a.
\(y'=\dfrac{1}{2\sqrt{x-3}}-\dfrac{1}{2\sqrt{6-x}}=\dfrac{\sqrt{6-x}-\sqrt{x-3}}{2\sqrt{\left(x-3\right)\left(6-x\right)}}\)
\(y'=0\Rightarrow6-x=x-3\Rightarrow x=\dfrac{9}{2}\)
\(x=\dfrac{9}{2}\) là điểm cực đại của hàm số
b.
\(y'=1-\dfrac{9}{\left(x-2\right)^2}=0\Rightarrow\left(x-2\right)^2=9\Rightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
\(x=-1\) là điểm cực đại, \(x=5\) là điểm cực tiểu
c.
\(y'=\sqrt{3-x}-\dfrac{x}{2\sqrt{3-x}}=0\Rightarrow2\left(3-x\right)-x=0\)
\(\Rightarrow x=2\)
\(x=2\) là điểm cực đại
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
d.
\(y'=\dfrac{-x^2+4}{\left(x^2+4\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
\(x=-2\) là điểm cực tiểu, \(x=2\) là điểm cực đại
e.
\(y'=\dfrac{-8\left(x^2-5x+4\right)}{\left(x^2-4\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
\(x=1\) là điểm cực tiểu, \(x=4\) là điểm cực đại
CM
30 tháng 3 2018
Chọn D
Hàm số có 2 điểm cực trị x 1 , x 2
Chia y cho y’ ta được :
Điểm cực trị tương ứng :
Với x 1 + x 2 = 4 x 1 x 2 = m + 2 nên y 1 y 2 = ( m - 2 ) 2 ( 4 m + 17 )
Hai cực trị cùng dấu ⇔ y 1 y 2 > 0
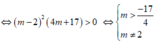
Kết hợp đk : - 17 4 < m < 2
PT
1
CM
30 tháng 10 2019
TXĐ: R
y′ = 2(x + 2). x - 3 3 + 3 x + 2 2 . x - 3 2 = 5x(x + 2). x - 3 2
y′= 0 ⇔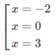 
Bảng biến thiên:
Từ đó suy ra y CĐ = y(-2) = 0; y CT = y(0) = -108.
PT
1
CM
27 tháng 4 2019
Hàm số xác định trên khoảng (− ∞ ;+ ∞ ).
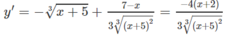
Bảng biến thiên:
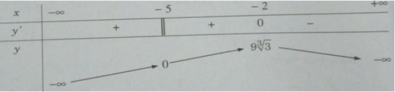
Vậy
y
CD
= y(−2) =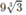 
TXĐ: D = (− ∞ ; − 6 ) ∪ ( 6 ; + ∞ )
Bảng biến thiên:
Từ đó ta thấy hàm số đạt cực đại tại x = -3, đạt cực tiểu tại x = -3 và y CT = y(3) = 9 3 ; y CD = y(−3) = −9 3