NM
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
P
1
AH
Akai Haruma
Giáo viên
31 tháng 3 2023
Lời giải:
$xy+12=x+y$
$\Rightarrow xy-x-y=-12$
$\Rightarrow x(y-1)-y=-12$
$\Rightarrow x(y-1)-(y-1)=-11$
$\Rightarrow (y-1)(x-1)=-11$
Do $x,y$ nguyên nên $x-1,y-1$ cũng nguyên. Ta có bảng: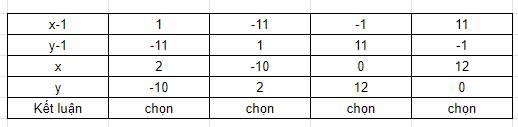
NA
2
21 tháng 4 2021
\(x^2-xy+y+1=0\)
\(\Leftrightarrow\left(x^2-1\right)-y\left(x-1\right)+2=0\)
\(\Leftrightarrow\left(x+1-y\right)\left(x-1\right)=-2\)
\(\Rightarrow x-1;x+1-y\inƯ\left(-2\right)=\left\{\pm1;\pm2\right\}\)
| x - 1 | 1 | -1 | 2 | -2 |
| x + 1 - y | 2 | -2 | 1 | -1 |
| x | 2 | 0 | 3 | -1 |
| y | 1 | 3 | 3 | 1 |
21 tháng 4 2021
bảng mình xét nhầm nhé phải là như này :
| x - 1 | 1 | -1 | 2 | -2 |
| x + 1 - y | -2 | 2 | -1 | 1 |
| x | 2 | 0 | 3 | -1 |
| y | 5 | -1 | 5 | 1 |
LY
24 tháng 8 2016
11=1x11=11x1=-1x-11=-11x-1
TH1:
2x-1=1 y+4=11
2x=2 y=7
x=1
TH2:
2x-1=11 y+4=1
2x=12 y=-5
x=6
TH3:
2x-1=-1 y+4=-11
2x=-2 y=-15
x=-1
TH4:
2x-1=-11 y+4=-1
2x=-10 y=-5
x=-5
NT
4
10 tháng 3 2016
xy=x+y
=> x(y-1)=y (*)
=> x=y/(y-1)
Để x nguyên thì y chia hết cho y-1
do y, y-1 luôn nguyên tố cùng nhau với y-1>=2 hoặc y-1<=-2
=> y-1=1 hoặc y-1=-1
TH1: Nếu y-1=1
=>y=2
(*) => x=2
TH2 :Nếu y-1=-1 => y=0 và x=0
Vậy có cặp số nguyên (x;y) =(2,2) và (0,0).
ND
1
23 tháng 12 2015
x +y = xy
<=>x(1-y)=y
<=>x=y/(1-y)=1/(1-y) -1
để x nguyên
=>1/(1-y) nguyên
=>1-y là ước của 1.
=>
+)1-y=1
<=>y=0 và x=0
+)1-y=-1
<=>y=2 và x=2
vậy hệ có 2 nghiệm nguyên:
(0;0) và (2;2)
28 tháng 10 2023
4:
(x+1)(y-2)=5
=>\(\left(x+1;y-2\right)\in\left\{\left(1;5\right);\left(5;1\right);\left(-1;-5\right);\left(-5;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(0;7\right);\left(4;3\right);\left(-2;-3\right);\left(-6;1\right)\right\}\)
DT
1
19 tháng 4 2019
\(\Rightarrow2xy-6=x\)
\(\Rightarrow2xy-x=6\)
\(\Rightarrow x.\left(2y-1\right)=6\)
Vì \(x,y\in Z\Rightarrow x,2y-1\in Z\)
mà \(6=3.2=2.3=-2.\left(-3\right)=-3.\left(-2\right)\)
Lập bảng ra rồi loại trừ tìm x,y
CH
Cô Hoàng Huyền
Admin
VIP
1 tháng 2 2018
a) Ta có : \(x+y+xy=0\Rightarrow x+xy+y+1=1\)
\(\Rightarrow x\left(y+1\right)+\left(y+1\right)=1\Rightarrow\left(x+1\right)\left(y+1\right)=1\)
Vậy thì x + 1 và y + 1 phải là ước của 1.
Ta có bảng:
| x + 1 | 1 | -1 |
| y + 1 | 1 | -1 |
| x | 0 | -2 |
| y | 0 | -2 |
Vậy ta tìm được các cặp (x;y) = (0 ; 0) và (-2 ; -2).
b)
Ta có : \(x-y-xy=0\Rightarrow x-xy+1-y=1\)
\(\Rightarrow x\left(1-y\right)+\left(1-y\right)=1\Rightarrow\left(x+1\right)\left(1-y\right)=1\)
Vậy thì x + 1 và 1 - y phải là ước của 1.
Ta có bảng:
| x + 1 | 1 | -1 |
| 1 - y | 1 | -1 |
| x | 0 | -2 |
| y | 0 | 1 |
Vậy ta tìm được các cặp (x;y) thỏa mãn là (0;0) và (-2;1)
SH
3
25 tháng 2 2020
Ta có: \(xy+3x-y-3=0\)
\(\Rightarrow\)xy + 3x - y = 6
=>x(y+3) - y = 6
=>x(y+3) - y - 3 = 3
=>x(y+3) - (y+3) = 3
=> (y+3)(x-1) =3
Vì x, y là các số nguyên nên y+3;x-1 là các số nguyên
Ta có bảng sau:
| y+3 | -3 | -1 | 1 | 3 |
| y | -6 | -4 | -2 | 0 |
| x-1 | -1 | -3 | 3 | 1 |
| x | 0 | -2 | 4 | 2 |