PH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
22 tháng 1
a, Để \(\dfrac{n+1}{n-2}\) có giá trị là một số nguyên thì n + 1 ⋮ n - 2
=> (n - 2) + 3 ⋮ n - 2
Vì (n - 2) ⋮ n - 2 nên 3 ⋮ n - 2
=> n - 2 ∈ Ư(3) ∈ {-3;-1;1;3}
=> n ∈ {-1;1;3;5}
b, Để \(\dfrac{4n+5}{2n-1}\) có giá trị là một số nguyên thì 4n + 5 ⋮ 2n - 1
=> (4n - 2) + 7 ⋮ 2n - 1
=> 2(2n - 1) + 7 ⋮ 2n - 1
Vì 2(2n - 1) ⋮ 2n -1 nên 7 ⋮ 2n - 1
=> 2n - 1 ∈ Ư(7) ∈ {-7;-1;1;7}
=> n ∈ {-3;0;1;4}
NA
1
23 tháng 1 2022
a: Để A nguyên thì \(n-1\in\left\{1;-1;3;-3\right\}\)
hay \(n\in\left\{2;0;4;-2\right\}\)
b: Để B nguyên thì \(3n+1\in\left\{1;4\right\}\)
hay \(n\in\left\{0;1\right\}\)
c: Để C nguyên thì \(n+3⋮2n-1\)
\(\Leftrightarrow2n+6⋮2n-1\)
\(\Leftrightarrow2n-1\in\left\{1;-1;7;-7\right\}\)
hay \(n\in\left\{1;0;4;-3\right\}\)
PT
1
23 tháng 6 2021
Câu 1:
a) \(\dfrac{n-5}{n-3}\)
Để \(\dfrac{n-5}{n-3}\) là số nguyên thì \(n-5⋮n-3\)
\(n-5⋮n-3\)
\(\Rightarrow n-3-2⋮n-3\)
\(\Rightarrow2⋮n-3\)
\(\Rightarrow n-3\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
Ta có bảng giá trị:
| n-1 | -2 | -1 | 1 | 2 |
| n | -1 | 0 | 2 | 3 |
Vậy \(n\in\left\{-1;0;2;3\right\}\)
b) \(\dfrac{2n+1}{n+1}\)
Để \(\dfrac{2n+1}{n+1}\) là số nguyên thì \(2n+1⋮n+1\)
\(2n+1⋮n+1\)
\(\Rightarrow2n+2-1⋮n+1\)
\(\Rightarrow1⋮n+1\)
\(\Rightarrow n-1\inƯ\left(1\right)=\left\{\pm1\right\}\)
Ta có bảng giá trị:
| n-1 | -1 | 1 |
| n | 0 | 2 |
Vậy \(n\in\left\{0;2\right\}\)
23 tháng 6 2021
Câu 2:
a) \(\dfrac{n+7}{n+6}\)
Gọi \(ƯCLN\left(n+7;n+6\right)=d\)
\(\Rightarrow\left[{}\begin{matrix}n+7⋮d\\n+6⋮d\end{matrix}\right.\)
\(\Rightarrow\left(n+7\right)-\left(n+6\right)⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
Vậy \(\dfrac{n+7}{n+6}\) là p/s tối giản
b) \(\dfrac{3n+2}{n+1}\)
Gọi \(ƯCLN\left(3n+2;n+1\right)=d\)
\(\Rightarrow\left[{}\begin{matrix}3n+2⋮d\\n+1⋮d\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}3n+2⋮d\\3.\left(n+1\right)⋮d\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}3n+2⋮d\\3n+3⋮d\end{matrix}\right.\)
\(\Rightarrow\left(3n+3\right)-\left(3n+2\right)⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=1\)
Vậy \(\dfrac{3n+2}{n+1}\) là p/s tối giản
28 tháng 6 2023
a: 12/3n-1 là số nguyên khi 3n-1 thuộc Ư(12)
=>3n-1 thuộc {1;-1;2;-2;3;-3;4;-4;6;-6;12;-12}
mà n là số nguyên
nên n thuộc {0;1;-1}
c: 2n+5/n-3 là số nguyên
=>2n-6+11 chia hết cho n-3
=>n-3 thuộc {1;-1;11;-11}
=>n thuộc {4;2;14;-8}
DA
2 tháng 3 2020
Để \(\frac{10}{2n-3}\)là số nguyên thì 10 \(⋮\)2n-3
=> 2n -3 thuộc Ư(10) ={ 1; 2; 5; 10; -1; -2; -5; -10}
Vì 2n-3 là số lẻ nên 2n-3 \(\in\){1; -1; 5; -5}
=> 2n \(\in\){ 4; 2; 8; -2}
=> n \(\in\){ 2; 1; 4; -1}
Vậy...
2 tháng 3 2020
a)Để \(\frac{10}{2n+3}\)là một số nguyên thì \(10⋮2n+3\)
=>\(2n+3\inƯ\left(10\right)=\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
+)Ta có bảng:
| 2n+3 | -1 | 1 | -2 | 2 | -5 | 5 | -10 | 10 |
| n | -2\(\in Z\) | -1\(\in Z\) | -2,5\(\notin Z\) | -0,5\(\notin Z\) | -4\(\in Z\) | 1\(\in Z\) | -6,5\(\notin Z\) | 3,5\(\notin Z\) |
Vậy n\(\in\){-2;-1;-4;1}
Chúc bn học tốt
2 tháng 3 2023
a: Để A là phân số thì n-2<>0
=>n<>2
Khi n=-2 thì \(A=\dfrac{2\cdot\left(-2\right)+1}{-2-2}=\dfrac{-3}{-4}=\dfrac{3}{4}\)
b: Để A nguyên thì 2n+1 chia hết cho n-2
=>2n-4+5 chia hết cho n-2
=>\(n-2\in\left\{1;-1;5;-5\right\}\)
=>\(n\in\left\{3;1;7;-3\right\}\)
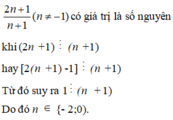
\(\frac{2n+3}{n+2}=\frac{2n+4-1}{n+2}=2-\frac{1}{n+2}\inℤ\)
mà \(n\inℤ\Rightarrow n+2\inƯ\left(1\right)=\left\{-1;1\right\}\Leftrightarrow n\in\left\{-3;-1\right\}\).