Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
lim x → 2 − f x = lim x → 2 − a x − 1 = 2 a − 1 lim x → 2 + f x = lim x → 2 + x − 2 + 3 = 3
Hàm số có giới hạn tại x=2 ⇔ lim x → 2 − f x = lim x → 2 + f x ⇔ 2 a − 1 = 3 ⇔ a = 2
Chọn đáp án A

Ta có :
lim x → 1 − f x = lim x → 1 − m − 3 = m − 3 lim x → 1 + f x = lim x → 1 + 1 − 7 x 2 + 2 = − 2
Để tồn tại lim x → 1 f ( x ) khi và chỉ khi:
lim x → 1 − f x = lim x → 1 + f x ⇔ m − 3 = − 2 ⇔ m = 1
Chọn đáp án B

- Hàm số đã cho xác định trên R.
- Ta có:
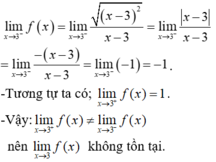
- Vậy với mọi m, hàm số đã cho không liên tục tại x = 3.
Do đó đáp án đúng là A.

3.
\(x-2y+1=0\Leftrightarrow y=\frac{1}{2}x+\frac{1}{2}\)
\(y'=\frac{2}{\left(x+1\right)^2}\Rightarrow\frac{2}{\left(x+1\right)^2}=\frac{1}{2}\)
\(\Rightarrow\left(x+1\right)^2=4\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-3\Rightarrow y=3\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}y=\frac{1}{2}\left(x-1\right)+1\\y=\frac{1}{2}\left(x+3\right)+3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}y=\frac{1}{2}x+\frac{1}{2}\left(l\right)\\y=\frac{1}{2}x+\frac{9}{2}\end{matrix}\right.\)
4.
\(\lim\limits\frac{\sqrt{2n^2+1}-3n}{n+2}=\lim\limits\frac{\sqrt{2+\frac{1}{n^2}}-3}{1+\frac{2}{n}}=\sqrt{2}-3\)
\(\Rightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)
5.
\(\lim\limits_{x\rightarrow a}\frac{2\left(x^2-a^2\right)+a\left(a+1\right)-\left(a+1\right)x}{\left(x-a\right)\left(x+a\right)}=\lim\limits_{x\rightarrow a}\frac{\left(x-a\right)\left(2x+2a\right)-\left(a+1\right)\left(x-a\right)}{\left(x-a\right)\left(x+a\right)}\)
\(=\lim\limits_{x\rightarrow a}\frac{\left(x-a\right)\left(2x+a-1\right)}{\left(x-a\right)\left(x+a\right)}=\lim\limits_{x\rightarrow a}\frac{2x+a-1}{x+a}=\frac{3a-1}{2a}\)
1.
\(f'\left(x\right)=-3x^2+6mx-12=3\left(-x^2+2mx-4\right)=3g\left(x\right)\)
Để \(f'\left(x\right)\le0\) \(\forall x\in R\) \(\Leftrightarrow g\left(x\right)\le0;\forall x\in R\)
\(\Leftrightarrow\Delta'=m^2-4\le0\Rightarrow-2\le m\le2\)
\(\Rightarrow m=\left\{-1;0;1;2\right\}\)
2.
\(f'\left(x\right)=\frac{m^2-20}{\left(2x+m\right)^2}\)
Để \(f'\left(x\right)< 0;\forall x\in\left(0;2\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-20< 0\\\left[{}\begin{matrix}m>0\\m< -4\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-\sqrt{20}< m< \sqrt{20}\\\left[{}\begin{matrix}m>0\\m< -4\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m=\left\{1;2;3;4\right\}\)

\(f\left(x\right)=-x^3-2x^2+mx-3\)
\(f'\left(x\right)=-3x^2-4x+m\)
\(f'\left(x\right)>0\Leftrightarrow-3x^2-4x+m>0\Leftrightarrow m>3x^2+4x\)(đúng với mọi \(x\in\left(0,1\right)\))
suy ra \(m\ge max\left(3x^2+4x\right)\)với \(x\in\left[0,1\right]\).
Xét hàm \(g\left(x\right)=3x^2+4x\)với \(x\in\left[0,1\right]\).
\(g'\left(x\right)=6x+4\)
\(g'\left(x\right)=0\Leftrightarrow6x+4=0\Leftrightarrow x=-\frac{2}{3}\notin\left[0,1\right]\).
\(g\left(0\right)=0,g\left(1\right)=7\)
suy ra \(g_{max}=7\)
do đó \(m\ge7\).
Mà \(m\)nguyên, \(m\in\left[-2021,2021\right]\)nên có tổng cộng: \(2021-7+1=2015\)giá trị của \(m\)thỏa mãn.

\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\sqrt{2x-4}+3\)
\(=\sqrt{2\cdot2-4}+3=3\)
\(f\left(2\right)=\sqrt{2\cdot2-4}+3=0+3=3\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\dfrac{x+2}{x^2-2mx+m^2+2}\)
\(=\dfrac{2+2}{2^2-2m\cdot2+m^2+2}=\dfrac{4}{m^2-4m+6}\)
Để hàm số f(x) liên tục trên R thì f(x) liên tục tại x=2
=>\(\dfrac{4}{m^2-4m+6}=3\)
=>\(4=3\left(m^2-4m+6\right)\)
=>\(3m^2-12m+18-4=0\)
=>\(3m^2-12m+14=0\)
\(\Leftrightarrow3m^2-12m+12+2=0\)
=>\(3\left(m-2\right)^2+2=0\)(vô lý)
=>\(m\in\varnothing\)

\(f'\left(x\right)=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Để \(g\left(x\right)_{min}>0\Rightarrow f\left(x\right)=0\) vô nghiệm trên đoạn đã cho
\(\Rightarrow\left[{}\begin{matrix}-m< -2\\-m>7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m>2\\m< -7\end{matrix}\right.\)
\(g\left(0\right)=\left|m-1\right|\) ; \(g\left(1\right)=\left|m-2\right|\) ; \(g\left(2\right)=\left|m+7\right|\)
Khi đó \(g\left(x\right)_{min}=min\left\{g\left(0\right);g\left(1\right);g\left(2\right)\right\}=min\left\{\left|m-2\right|;\left|m+7\right|\right\}\)
TH1: \(g\left(x\right)_{min}=g\left(0\right)\Leftrightarrow\left\{{}\begin{matrix}\left|m-2\right|\le\left|m+7\right|\\\left|m-2\right|=2020\\\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ge\dfrac{5}{2}\\\left|m-2\right|=2020\end{matrix}\right.\) \(\Rightarrow m=2022\)
TH2: \(g\left(x\right)_{min}=g\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}\left|m+7\right|\le\left|m-2\right|\\\left|m+7\right|=2020\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\le\dfrac{5}{2}\\\left|m+7\right|=2020\end{matrix}\right.\) \(\Rightarrow m=-2027\)
Ta có :
lim x → 3 − f x = lim x → 3 − m = m lim x → 3 + f x = lim x → 3 + 3 − x x + 1 − 2 = lim x → 3 + ( 3 − x ) . ( x + 1 + 2 ) x − 3 = lim x → 3 + − ( x + 1 + 2 ) = − 4
Vậy để tồn tại lim x → 3 f x khi và chỉ khi :
lim x → 3 − f x = lim x → 3 + f x ⇔ m = − 4
Chọn đáp án C