K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 10 2021
\(=\left|\sqrt{11}-3\right|-\left|\sqrt{11}-4\right|=\sqrt{11}-3+\sqrt{11}-4=-7+2\sqrt{11}\)
1 tháng 10 2021
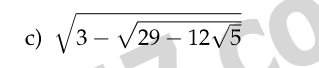
\(\sqrt{3-\sqrt{29-12\sqrt{5}}}=\sqrt{3-\sqrt{\left(2\sqrt{5}-3\right)^2}}=\sqrt{3-2\sqrt{5}+3}=\sqrt{6-2\sqrt{5}}=\sqrt{\left(\sqrt{5}-1\right)^2}=\sqrt{5}-1\)
1 tháng 10 2021
\(=\sqrt{3-\sqrt{\left(2\sqrt{5}-3\right)^2}}=\sqrt{3-2\sqrt{5}+3}=\sqrt{9-2\sqrt{5}}\)
MN
2
1 tháng 1 2022
\(\dfrac{5\sqrt{2}-\sqrt{8}+\sqrt{32}}{\sqrt{2}}=\dfrac{5\sqrt{2}-2\sqrt{2}+4\sqrt{2}}{\sqrt{2}}=\dfrac{7\sqrt{2}}{\sqrt{2}}=7\)
1 tháng 1 2022
`(5sqrt2-sqrt8+sqrt32):sqrt2`
`= \frac{5sqrt2}{sqrt2}-\frac{sqrt8}{sqrt2}+\frac{sqrt32}{sqrt2}`
`= 5-sqrt4+sqrt16`
`= 5-2+4`
`= 7`
18 tháng 8 2023
\(=\sqrt{4\sqrt{3}+2\left(2-\sqrt{3}\right)}\)
\(=\sqrt{4\sqrt{3}+4-2\sqrt{3}}\)
\(=\sqrt{4+2\sqrt{3}}=\sqrt{3}+1\)
CM
12 tháng 7 2017
x + 2 x - 3 = x - x + 3 x - 3 = x ( x - 1) + 3( x - 1) = ( x - 1)( x + 3)
a) Với điểu kiện x ≥ 0; x ≠ 1 ta có:
AT
2
AD
23 tháng 7 2023
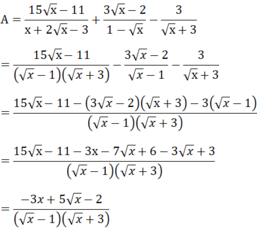
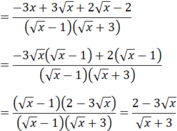
\(\dfrac{4}{\sqrt{7}+\sqrt{3}}+\dfrac{4}{\sqrt{7}-\sqrt{3}}\\ =\dfrac{4\left(\sqrt{7}-\sqrt{3}\right)}{\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)}+\dfrac{4\left(\sqrt{7}+\sqrt{3}\right)}{\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)}\\ =\dfrac{4\left(\sqrt{7}-\sqrt{3}\right)}{7-3}+\dfrac{4\left(\sqrt{7}+\sqrt{3}\right)}{7-3}\\ =\dfrac{4\left(\sqrt{7}-\sqrt{3}\right)}{4}+\dfrac{4\left(\sqrt{7}+\sqrt{3}\right)}{4}\\ =\sqrt{7}-\sqrt{3}+\sqrt{7}+\sqrt{3}\\ =2\sqrt{7}\)
@seven
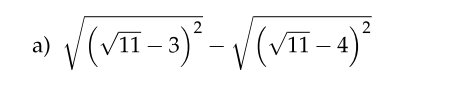
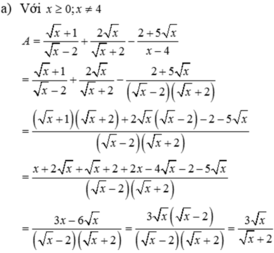
\(\dfrac{2}{\sqrt{3}-1}-\dfrac{4}{1+\sqrt{5}}-\left(\sqrt{3}-\sqrt{5}\right)=\dfrac{2\left(\sqrt{3}+1\right)}{3-1}-\dfrac{4\left(1-\sqrt{5}\right)}{1-5}-\sqrt{3}+\sqrt{5}=\sqrt{3}+1+1-\sqrt{5}-\sqrt{3}+\sqrt{5}=2\)