
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2.1
ĐKXĐ: \(x\ge-\dfrac{1}{16}\)
\(x^2-x-20-2\left(\sqrt{16x+1}-9\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4\right)-\dfrac{32\left(x-5\right)}{\sqrt{16x+1}+9}=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+4-\dfrac{32}{\sqrt{16x+1}+9}\right)=0\) (1)
Do \(x\ge-\dfrac{1}{16}\Rightarrow\left\{{}\begin{matrix}\dfrac{32}{\sqrt{16x+1}+9}< \dfrac{32}{9}\\x+4\ge-\dfrac{1}{16}+4=\dfrac{63}{16}>\dfrac{32}{9}\end{matrix}\right.\)
\(\Rightarrow x+4-\dfrac{32}{\sqrt{16x+1}+9}>0\)
Nên (1) tương đương:
\(x-5=0\)
\(\Leftrightarrow x=5\)
Câu 2.2, 2.3 đề lỗi không dịch được


2.2 Đề lỗi không dịch được
2.3
\(\Delta'=4m^2-2\left(2m^2-1\right)=2>0\Rightarrow\) pt luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=\dfrac{2m^2-1}{2}\end{matrix}\right.\)
\(\Rightarrow\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=2\Rightarrow\left[{}\begin{matrix}x_1-x_2=\sqrt{2}\\x_1-x_2=-\sqrt{2}\end{matrix}\right.\)
Do \(x_1\) là nghiệm của pt nên ta có:
\(2x_1^2-4mx_1+2m^2-1=0\Rightarrow2x_1^2=4mx_1-2m^2+1\)
Thế vào bài toán:
\(4mx_1-2m^2+1-4mx_2+2m^2-9< 0\)
\(\Leftrightarrow m\left(x_1-x_2\right)< 2\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2}m< 2\\-\sqrt{2}m< 2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< \sqrt{2}\\m>-\sqrt{2}\end{matrix}\right.\)
(Bản thân câu này đề bài cũng rất dở)

6. \(\hept{\begin{cases}x^2-3x=y\\y^2-3y=x\end{cases}}\)
\(\Rightarrow x^2-3y-y^2+3x=y-x\)
\(\Leftrightarrow\left(x-y\right)\left(x+y\right)+3\left(x-y\right)+\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+y+3+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-y=0\\x+y+4=0\end{cases}}\)
TH1 : x - y = 0 <=> x = y ta có : \(x^2-3x=x\) \(\Leftrightarrow x\left(x-4\right)=0\Leftrightarrow\orbr{\begin{cases}x=0=y\\x=4=y\end{cases}}\)
TH2 : x + y + 4 = 0 <=> y = -4-x ta có : \(x^2-3x=-x-4\)
\(\Leftrightarrow x^2-2x+4=0\)
\(\Leftrightarrow\left(x-1\right)^2+3=0\left(vonghiem\right)\)
12. \(\hept{\begin{cases}x^3+x^2y=10y\\y^3+xy^2=10x\end{cases}}\)
\(\Leftrightarrow x^3-y^3+x^2y-xy^2=10y-10x\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2\right)+xy\left(x-y\right)+10\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+2xy+y^2+10\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left[\left(x+y\right)^2+10\right]=0\)
mà có \(\left(x+y\right)^2+10>0\)
\(\Rightarrow x-y=0\Leftrightarrow x=y\)
ta có : \(x^3+x^3=10x\)
\(\Leftrightarrow2x^3-10x=0\Leftrightarrow2x\left(x^2-5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0=y\\x=\pm\sqrt{5}=y\end{cases}}\)
mấy cái hệ đối xứng này lấy pt trên trừ dưới là ra thôi, thể nào cũng có nghiệm x=y


Ta có: \(AB\perp CD\Rightarrow\) H là trung điểm CD (t/c bán kính vuông góc dây cung)
\(\Rightarrow\Delta ACD\) cân tại A (AH đồng thời là trung tuyến và đường cao)
\(\Rightarrow\widehat{ACD}=\widehat{ADC}\)
Mà \(\widehat{ADC}=\widehat{MCA}\) (cùng chắn AC)
\(\Rightarrow\widehat{ACD}=\widehat{MCA}\Rightarrow CA\) là phân giác của \(\widehat{MCD}\)
Áp dụng định lý phân giác trong tam giác MCH:
\(\dfrac{AM}{AH}=\dfrac{CM}{CH}\) (1)
Lại có \(\widehat{ACB}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ACB}=90^0\)
\(\Rightarrow CB\perp CA\)
\(\Rightarrow CB\) là đường phân giác ngoài góc \(\widehat{MCD}\) của tam giác MCH
Áp dụng định lý phân giác: \(\dfrac{BM}{BH}=\dfrac{CM}{CH}\) (2)
(1);(2) \(\Rightarrow\dfrac{AM}{AH}=\dfrac{BM}{BH}\Rightarrow BM.AH=BH.AM\)

1.
Xét pt đầu:
\(x^2-xy+x-y=0\)
\(\Leftrightarrow x\left(x-y\right)+x-y=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-y\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=y\end{matrix}\right.\)
TH1: \(x=-1\) thay xuống pt dươi:
\(\sqrt{y^2+15}=-3-2+\sqrt{9}\Leftrightarrow\sqrt{y^2+15}=-2< 0\) (vô nghiệm)
TH2: thay \(y=x\) xuống pt dưới:
\(\sqrt{x^2+15}=3x-2+\sqrt{x^2+8}\) (1)
\(\Rightarrow3x-2=\sqrt{x^2+15}-\sqrt{x^2+8}=\dfrac{7}{\sqrt{x^2+15}+\sqrt{x^2+8}}>0\)
\(\Rightarrow x>\dfrac{2}{3}\)
Do đó (1) tương đương:
\(3x-2+\sqrt{x^2+8}-\sqrt{x^2+15}=0\)
\(\Leftrightarrow3x-3+\sqrt{x^2+8}-3+4-\sqrt{x^2+15}=0\)
\(\Leftrightarrow3\left(x-1\right)+\dfrac{\left(x-1\right)\left(x+1\right)}{\sqrt{x^2+8}+3}-\dfrac{\left(x-1\right)\left(x+1\right)}{\sqrt{x^2+15}+4}=0\)
\(\Leftrightarrow\left(x-1\right)\left[3+\left(x+1\right)\left(\dfrac{1}{\sqrt{x^2+8}+3}-\dfrac{1}{\sqrt{x^2+15}+4}\right)\right]=0\)
\(\Leftrightarrow x-1=0\) (do \(x+1>0\) nên ngoặc phía sau luôn dương)
\(\Leftrightarrow x=y=1\)
2.
Pt đầu tương đương:
\(y^2-x+x^2-2xy+x=0\)
\(\Leftrightarrow\left(x-y\right)^2=0\Leftrightarrow y=x\)
Thay xuống pt dưới:
\(2x^2+x-x^2+x-3=0\)
\(\Leftrightarrow x^2+2x-3=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-3\Rightarrow y=-3\end{matrix}\right.\)


a: Theo đề, ta có: a*0+b=50000 và 2a+b=60000
=>b=50000 và a=5000
=>s=5000t+50000
b: Nếu không là hội viên thì phải trả:
90000-50000=40000(đồng)





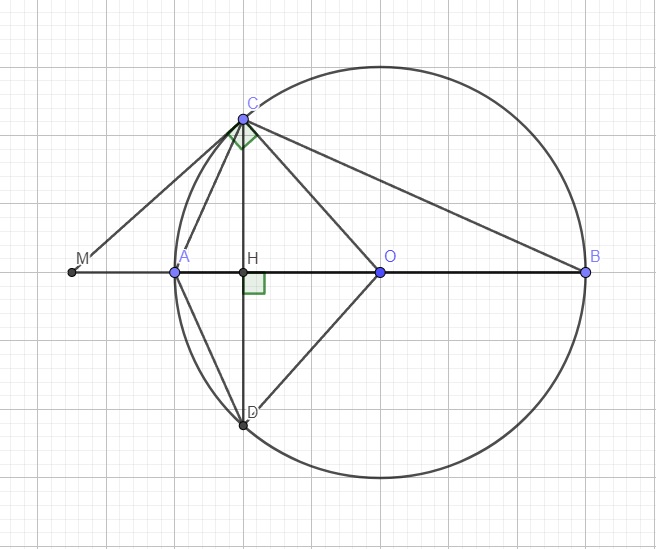



Đương nhiên là đường phân giác, vì khi kẻ 2 đường vuông góc sẽ tạo ra 2 tam giác vuông. Để 2 tam giác vuông đồng dạng chúng cần thêm 1 cặp góc bằng nhau khác, và luôn có thể tạo ra cặp góc bằng nhau từ 1 đường phân giác.