Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

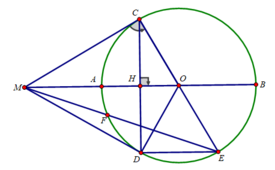
d) Ta có: ∠(CFE) = 90 0 (F thuộc đường tròn đường kính CE)
Lại có CF là đường cao nên MC 2 = MF.ME
Tương tự, ta có: MC 2 = MH.MO
⇒ ME.MF = MH.MO
⇒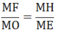
Xét ΔMOF và ΔMEN có:
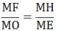
∠(FMO) chung
⇒ ΔMOF ∼ ΔMEN (c.g.c)
⇒ ∠(MOF) = ∠(MEH)

a) Xét (O) có
\(\widehat{ACB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{ACB}=90^0\)(Hệ quả góc nội tiếp)
Xét tứ giác EHAC có
\(\widehat{EHA}\) và \(\widehat{ECA}\) là hai góc đối
\(\widehat{EHA}+\widehat{ECA}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: EHAC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Suy ra: \(\widehat{HEC}+\widehat{HAC}=180^0\)(hai góc đối)
mà \(\widehat{HAC}+\widehat{BAC}=180^0\)(Hai góc kề bù)
nên \(\widehat{HEC}=\widehat{CAB}\)(Đpcm)

a: Xét ΔOAK vuông tại K và ΔOBK vuông tại K có
OA=OB
OK chung
Do đó: ΔOAK=ΔOBK
Suy ra: \(\widehat{AOK}=\widehat{BOK}\)
Ta có: \(AB\perp CD\Rightarrow\) H là trung điểm CD (t/c bán kính vuông góc dây cung)
\(\Rightarrow\Delta ACD\) cân tại A (AH đồng thời là trung tuyến và đường cao)
\(\Rightarrow\widehat{ACD}=\widehat{ADC}\)
Mà \(\widehat{ADC}=\widehat{MCA}\) (cùng chắn AC)
\(\Rightarrow\widehat{ACD}=\widehat{MCA}\Rightarrow CA\) là phân giác của \(\widehat{MCD}\)
Áp dụng định lý phân giác trong tam giác MCH:
\(\dfrac{AM}{AH}=\dfrac{CM}{CH}\) (1)
Lại có \(\widehat{ACB}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ACB}=90^0\)
\(\Rightarrow CB\perp CA\)
\(\Rightarrow CB\) là đường phân giác ngoài góc \(\widehat{MCD}\) của tam giác MCH
Áp dụng định lý phân giác: \(\dfrac{BM}{BH}=\dfrac{CM}{CH}\) (2)
(1);(2) \(\Rightarrow\dfrac{AM}{AH}=\dfrac{BM}{BH}\Rightarrow BM.AH=BH.AM\)