Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

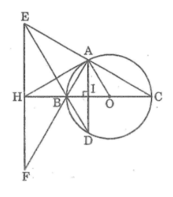
a, (O): góc BAC=90 độ (góc nt chắn nửa đường tròn).
(I): góc AEH=90(góc nt chắn nửa đường tròn). góc ADH=90(góc nt chắn nửa đường tròn) => tg AEHD là hcn(có 3 góc vuông)
b) (I): góc ADE=góc AHE( nt cùng chắn cung AE)
ta lại có:góc AHE=góc ABH( cùng phụ với góc BAH.) => ADE=ABH
=> tg BEDC nội tiếp (góc trong tại 1 đỉnh = góc ngoài tại đỉnh đối diện)
c, tg AEHD là hcn; AH cắt AD tại I => IA=IH=IE=ID
tam giác ADH: DI là trung tuyến
tam giác: AMH: MI là trung tuyến => D,M,I thẳng hàng. mà E,M,I thẳng hàng=> D,M,E thẳng hàng.
Nhớ L I K E nha

A B O C H D E F K M I J
Gọi giao điểm của AK và MB là I; giao điểm của IF với AB là J.
Xét tam giác vuông ICA ta thấy DA = DC nên DA = DC = DI.
Lại có DB là trung trực của AF nên DA = DF. Vậy thì DA = DF = DI hay tam giác IFA vuông tại F, suy ra DB // IJ.
Vậy thì DB là đường trung bình tam giác AIJ hay B là trung điểm AJ.
Ta có KF // AJ nên áp dụng Ta let ta có:
\(\frac{KM}{AB}=\frac{IM}{IB}=\frac{MF}{BJ}\)
Do AB = BJ nên KM = MF.

c) vì OK vg vs BC=>..............................................
d)