Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Phương pháp: Đặt t = 2 x
Cách giải: Đặt 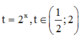 khi đó ta có
khi đó ta có 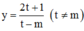 có
có  luôn đồng biến hoặc nghịch biến trên từng khoảng xác định của nó.
luôn đồng biến hoặc nghịch biến trên từng khoảng xác định của nó.
Để hàm số ban đầu nghịch biến trên (–1;1) => hàm số 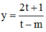 nghịch biến trên
nghịch biến trên 
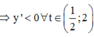 và
và 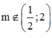
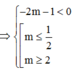
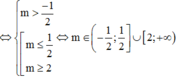
Kết hợp 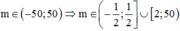
Vậy có tất cả 49 giá trị m nguyên thỏa mãn yêu cầu bài toán

Đáp án B
Do x ∈ - 1 ; 1 nên 0 ≤ x ≤ 1 . Do đó 2 0 ≤ 2 x ≤ 2 1 ⇒ 1 ≤ y ≤ 2 .
Giá trị nhỏ nhất của hàm số là 1 khi x = 0.

Đáp án C
TXĐ: D= R.
Ta có y′=(2x+2)ex+(x2+2x−2)ex=(x2+4x)ex=0⇔[x=−4x=0.
Ta có bảng biến thiên
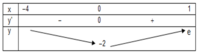
Vậy GTLN và GTNN của hàm số trên [0;1] lần lượt bằng e và −2.

Đáp án D
Xét hàm số y = x 3 - 3 m x 2 - 2 x - m trên khoảng (0;1) có y ' = 3 x 2 - 6 m x - 2
Hàm số đã cho liên tục và nghịch biến trên khoảng (0;1) khi và chỉ khi y ' ≤ 0 , ∀ x ∈ 0 ; 1
Khi đó 3 x 2 - 6 m x - 2 ≤ 0 ; ∀ x ∈ 0 ; 1 ⇔ 6 m ≥ 3 x 2 - 2 x ; ∀ x ∈ 0 ; 1 ⇔ 6 m ≥ m a x 0 ; 1 3 x 2 - 2 x
Xét hàm số f x = 3 x 2 - 2 x trên [0;1], ta có f ' x = 3 + 2 x 2 > 0 , ∀ x ∈ 0 ; 1 suy ra f(x) là hàm số đồng biến trên [0;1].
Do đó m a x 0 ; 1 f x = f 1 = 1 . Khi đó 6 m ≥ 1 ⇔ m ≥ 1 6 .
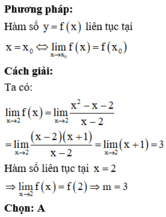




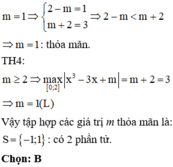
Đáp án C