Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Vì là hình lập phương nên các góc đều là góc vuông.
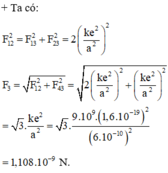
Đáp án A

Cùng đẩy trái hút, ta thấy q4 và q2 đẩy nhau, q1 và q2 hút nhau, q2 và q3 hút nhau.
\(F_{12}=\frac{k.\left|q_1q_2\right|}{r_{12}^2}=\frac{k.\left|q_1q_2\right|}{0,3^2}\left(N\right)=F_{23}\) \(\Rightarrow F_{123}=\sqrt{F_{12}^2+F_{23}^2}=...\)
\(F_{24}=\frac{k.\left|q_2q_4\right|}{r_{24}^2}=\frac{k.\left|q_2q_4\right|}{r_{12}^2+r_{14}^2}=\frac{k\left|q_1q_2\right|}{0,18}\left(N\right)\)
\(\Rightarrow\sum F=\left|F_{24}-F_{123}\right|=...\left(N\right)\) (do 2 lực này ngược chiều)

cạnh bằng 0,03m
\(q_1=18.10^{-8}C\)
\(q_3=-36.10^{-8}C\)
a)\(\overrightarrow{F}=\overrightarrow{F_{13}}+\overrightarrow{F_{23}}\)
\(\Leftrightarrow F=\sqrt{F^2_{13}+F_{23}^2+2.F_1.F_2.cos\left(\frac{45}{2}\right)}\) (4)
F13=\(\frac{k.\left|q_1.q_3\right|}{AC^2}\) (1)
\(F_{23}=\frac{k.\left|q_2.q_3\right|}{BC^2}\) (2)
AC=\(\frac{BC}{cos45^0}=\frac{3}{50\sqrt{2}}m\) (3)
từ (1),(2), (3), (4)
\(\Rightarrow F\approx\)0,95541N
b)
\(F_{34}=\frac{k.\left|q_3.q_4\right|}{DC^2}\)
\(F_{14}=\frac{k.\left|q_1.q_4\right|}{AD^2}\)
\(F_{24}=\frac{k.\left|q_2.q_4\right|}{BD^2}\)
BD=AC
\(\overrightarrow{F'}=\overrightarrow{F_{14}}+\overrightarrow{F_{34}}+\overrightarrow{F_{24}}\)
cho: \(\overrightarrow{F_{34}}+\overrightarrow{F_{14}}=\overrightarrow{F''}\)
\(\Leftrightarrow F''=\sqrt{F_{34}^2+F_{14}^2}\)\(\approx\)\(0,16099N\)
ta có F'=\(\sqrt{F''^2+F_{24}^2}\)\(\approx\)0,176356N

Các thông số đã biết: q1=q0; q2,3=-q0; q4=\(\frac {q_0} {2}\)

1)Các lực tác dụng lên q1 biểu diễn như hình vẽ
F21=F31 (vì q2,3=-q0) = \(k\frac {|-q_0q_0|} {a^2}=k\frac {q_{0}^2} {a^2}\)
F'=\(\sqrt { F_{21}^2+F_{31}^2+2F_{21}F_{31}cos60}\)=\(\sqrt3\)F21=\(\sqrt3 \)k\(\frac {q_0^2} {a^2}\)(1)
Xét tam giác vuông AOH có OA=\(\frac {AH} {cos30}\)=\(\frac {\frac {a} {2}} {\frac {\sqrt3} {2}}\)=\(\frac {a\sqrt3} {3}\)<=>OA2=\(\frac {a} {3}\)
<=>F41=\(k\frac {|0,5q_0q_0|} {OA^2}\)=\(k\frac {q_0^2} {2.\frac {a} {3}}\)=\(\frac 3 2 k\frac {q_0^2} {a^2}\)(2)
Vì \(\sqrt3 > \frac 3 2\) nên F'>F41
Lực điện tổng hợp tác dụng lên q1 có hướng cùng với hướng F' và có độ lớn F1= F'-F41=\((\sqrt3-\frac 3 2)k\frac {q_0^2} {a^2}\) , thay số q0=4.10-8C; a=4cm=0,04m
<=>F1≃2.088.10-3N
2)Các lực tác dụng lên q4 như hình vẽ:

F20=F30=\(k\frac {|0,5q_0(-q_0)|} {\frac a 3}\)=\(\frac 3 2k\frac {q_0^2} {a^2}\)=F24=F34
Vì BOC=120 nên hợp lực của F20 và F30 cũng có độ lớn F'=F20=\(\frac 3 2k\frac {q_0^2} {a^2}\)
F14=F41(ở trên)=\(\frac 3 2 k\frac {q_0^2} {a^2}\) (4 và 0 như nhau nhé bạn mình vẽ nhầm)
<=>Theo hình vẽ <=> F4=F14+F'=\(3k\frac {q_0^2} {a^2}\), thế số <=>F4=0,027N

Các điện tích q 1 v à q 2 tác dụng lên điện tích q 3 các lực F 1 → và F 2 → có phương chiều như hình vẽ:
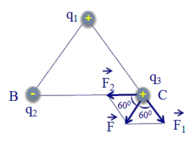
Có độ lớn: F 1 = F 2 = k | q 1 q 3 | A C 2 = 9 . 10 9 . | 4.10 − 8 .5.10 − 8 | ( 2.10 − 2 ) 2 = 45 . 10 - 3 (N).
Lực tổng hợp do q 1 v à q 2 tác dụng lên q 3 là:
F → = F 1 → + F 2 → ; có phương chiều như hình vẽ, có độ lớn:
F = F 1 cos 60 ° + F 2 cos 60 ° = 2 F 1 cos 60 ° = F 1 = 45 . 10 - 3 N .

Đáp án: A
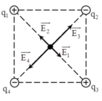
+ Cường độ điện trường tổng hợp tại tâm O của hình vuông:
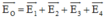
+ Trong đó E 1 → , E 2 → , E 3 → , E 4 → lần lượt là véctơ cường độ điện trường do các điện tích q 1 , q 2 , q 3 , q 4 gây ra tại O.
+ Để cường độ điện trường tại O triệt tiêu thì E O → = 0
+ Vì q 1 = q 3 và AO = CO nên: