
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a,\(6x^2+x-5=0\)
\(\Delta=b^2-4ac=1^2-4.6.\left(-5\right)=1+120=121\)
Vì \(\Delta>0\)nên pt có 2 nghiệm phân biệt
\(x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-1-\sqrt{121}}{2.6}=\frac{-1-11}{12}=\frac{-12}{12}=-1\)
\(x_2=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-1+\sqrt{121}}{2.6}=\frac{-1+11}{12}=\frac{10}{12}=\frac{5}{6}\)
Vậy \(S=\left\{-1;\frac{5}{6}\right\}\)
b, \(3x^2+4x+2=0\)
\(\Delta=b^2-4ac=4^2-4.3.2=16-24=-8\)
Vì \(\Delta< 0\)nên pt vô nghiệm
c, \(x^2-8x+16=0\)
\(\Delta=b^2-4ac=\left(-8\right)^2-4.1.16=64-64=0\)
Vì \(\Delta=0\)nên pt có nghiệm kép
\(x_1=x_2=\frac{-b}{2a}=\frac{-b'}{a}=\frac{8}{4}=\frac{4}{2}=2\)
a) \(6x^2+x-5=0\)
Ta có : \(\Delta=1+4.6.5=121>0\)
\(\Rightarrow\sqrt{\Delta}=11\)
Phương trình có hai nghiệm :
\(x_1=\frac{-1+11}{2.6}=\frac{5}{6}\)
\(x_2=\frac{-1-11}{2.6}=-1\)
b) \(3x^2+4x+2=0\)
Ta có : \(\Delta=4^2-4.3.2=-8< 0\)
Vậy phương trình vô nghiệm
c) \(x^2-8x+16=0\)
Ta có : \(\Delta=\left(-8\right)^2-4.1.16=0\)
Phương trình có nghiệm kép :
\(x_1=x_2=\frac{8}{2}=-4\)

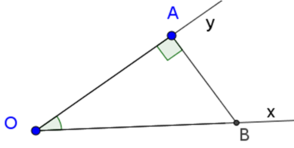
Dựng góc nhọn ∠xOy = α tùy ý.
Trên tia Ox lấy điểm B bất kì, kẻ BA ⊥ Oy (A ∈ Oy)
Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
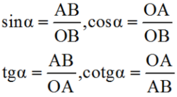

Bài 5:
\(x^2+2mx+2m-6=0\)
\(\text{Δ}=\left(2m\right)^2-4\left(2m-6\right)\)
\(=4m^2-8m+24\)
\(=4m^2-8m+4+20\)
\(=\left(2m-2\right)^2+20>=20>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-2m}{1}=-2m\\x_1x_2=\dfrac{c}{a}=\dfrac{2m-6}{1}=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=2x_1x_2+20\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2-2x_1x_2=20\)
=>\(\left(-2m\right)^2-4\left(2m-6\right)=20\)
=>\(4m^2-8m+24-20=0\)
=>\(4m^2-8m+4=0\)
=>\(\left(2m-2\right)^2=0\)
=>2m-2=0
=>2m=2
=>m=1(nhận)
Câu 4:
a: \(2x^2-2x-m=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot2\cdot\left(-m\right)\)
\(=4+8m\)
Để phương trình có hai nghiệm phân biệt thì 8m+4>0
=>8m>-4
=>\(m>-\dfrac{1}{2}\)
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-2\right)}{2}=\dfrac{2}{2}=1\\x_1x_2=\dfrac{c}{a}=\dfrac{-m}{2}\end{matrix}\right.\)
\(\left(1-x_1x_2\right)^2+4\cdot\left(x_1^2+x_2^2\right)=16\)
=>\(\left(1+\dfrac{m}{2}\right)^2+4\cdot\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=16\)
=>\(\left(\dfrac{m+2}{2}\right)^2+4\left[1^2-2\cdot\dfrac{-m}{2}\right]=16\)
=>\(\dfrac{1}{4}\left(m^2+4m+4\right)+4\left(1+m\right)=16\)
=>\(\dfrac{1}{4}m^2+m+1+4+4m-16=0\)
=>\(\dfrac{1}{4}m^2+5m-11=0\)
=>\(m^2+20m-44=0\)
=>(m+22)(m-2)=0
=>\(\left[{}\begin{matrix}m+22=0\\m-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-22\left(loại\right)\\m=2\left(nhận\right)\end{matrix}\right.\)
5.
\(\Delta'=1+2m\)
a.
Phương trình có 2 nghiệm pb khi:
\(1+2m>0\Rightarrow m>-\dfrac{1}{2}\)
b.
Khi pt có 2 nghiệm, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=-\dfrac{m}{2}\end{matrix}\right.\)
\(\left(1-x_1x_2\right)^2+4\left(x_1^2+x_2^2\right)=16\)
\(\Leftrightarrow\left(1-x_1x_2\right)^2+4\left(x_1+x_2\right)^2-8x_1x_2=16\)
\(\Leftrightarrow\left(1+\dfrac{m}{2}\right)^2+4.1^2+4m=16\)
\(\Leftrightarrow\dfrac{m^2}{4}+5m-11=0\Rightarrow\left[{}\begin{matrix}m=2\\m=-22< -\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)
5.
\(\Delta'=m^2-\left(2m-6\right)=\left(m-1\right)^2+5>0;\forall m\)
Pt luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=2x_1x_2+20\)
\(\Leftrightarrow\left(x_1+x_2\right)^2=4x_1x_2+20\)
\(\Leftrightarrow4m^2=4\left(2m-6\right)+20\)
\(\Leftrightarrow m^2-2m+1=0\Rightarrow m=1\)

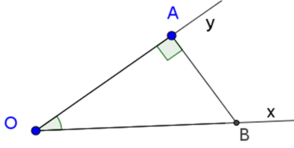
Dựng góc nhọn ∠xOy = α tùy ý.
Trên tia Ox lấy điểm B bất kì, kẻ BA ⊥ Oy (A ∈ Oy)
Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:

b) Áp dụng định lí pitago trong tam giác vuông OAB có:
O B 2 = O A 2 + A B 2
Từ đó ta có:
![]()


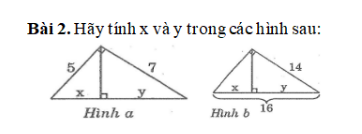 sử dụng định lí 1 và 2 giúp mik vs
sử dụng định lí 1 và 2 giúp mik vs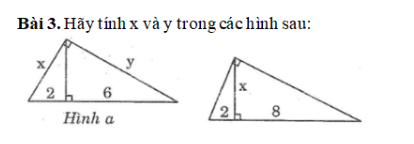 sử dụng định lý 1 và 2 giúp mik nha
sử dụng định lý 1 và 2 giúp mik nha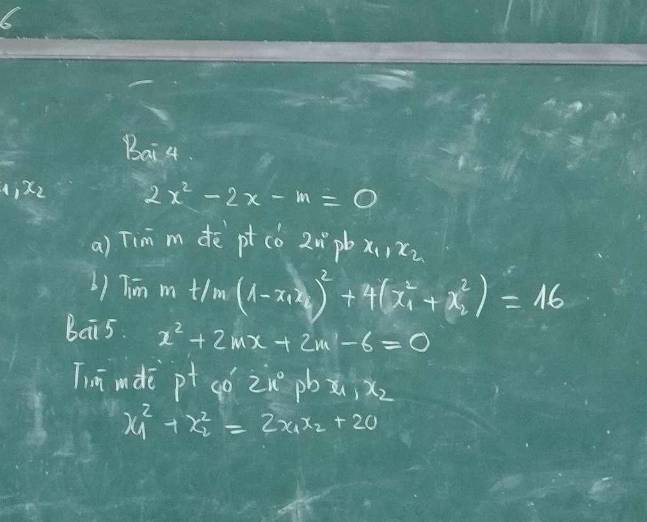
\(a,x+y=\sqrt{5^2+7^2}=\sqrt{74}\left(pytago\right)\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}5^2=x\sqrt{74}\\7^2=y\sqrt{74}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{25\sqrt{74}}{74}\\y=\dfrac{49\sqrt{74}}{74}\end{matrix}\right.\)
\(b,\) Áp dụng HTL:
\(14^2=16y\Leftrightarrow y=\dfrac{196}{16}=12,25\\ \Leftrightarrow x=16-12,25=3,75\)