K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TK
1
3 tháng 7 2021
a, \(\sqrt{15}+\sqrt{8}< \sqrt{16}+\sqrt{9}=4+3=7\)
\(\Rightarrow\sqrt{15}+\sqrt{8}< 7\)
b, \(\sqrt{10}+\sqrt{17}+1>\sqrt{9}+\sqrt{16}+1=3+4+1=8\)
\(\sqrt{61}< \sqrt{64}=8\)
\(\Rightarrow\sqrt{10}+\sqrt{17}+1>\sqrt{61}\)
c, \(\sqrt{10}+\sqrt{5}+1>\sqrt{9}+\sqrt{4}+1=3+2+1=6\)
\(\sqrt{35}< \sqrt{36}=6\)
\(\Rightarrow\sqrt{10}+\sqrt{5}+1>\sqrt{35}\)
22 tháng 8 2021
Bạn ơi, mik mới học lớp 8 thôi, bạn giải dùng nhiều kí tự mik ko hiểu, bạn có cách khác ko, hiện tại mik chỉ mới học hằng đẳng thức thôi ạ. Nhưng vẫn cảm ơn bạn rất nhiều bạn nha.
T
17 tháng 11 2023
\(\dfrac{4x+2}{4x-2}+\dfrac{3-6x}{6x-6}\left(dkxd:x\ne\dfrac{1}{2};x\ne1\right)\)
\(=\dfrac{2\left(2x+1\right)}{2\left(2x-1\right)}+\dfrac{3\left(1-2x\right)}{6\left(x-1\right)}\)
\(=\dfrac{2x+1}{2x-1}+\dfrac{1-2x}{2\left(x-1\right)}\)
\(=\dfrac{2x+1}{2x-1}+\dfrac{1-2x}{2x-2}\)
\(=\dfrac{\left(2x+1\right)\left(2x-2\right)}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{\left(1-2x\right)\left(2x-1\right)}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{4x^2-2x-2}{\left(2x-1\right)\left(2x-2\right)}+\dfrac{-4x^2+4x-1}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{4x^2-2x-2-4x^2+4x-1}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{2x-3}{\left(2x-1\right)\left(2x-2\right)}\)
\(=\dfrac{2x-3}{4x^2-6x+2}\)
NT
1
AH
Akai Haruma
Giáo viên
23 tháng 12 2022
Lời giải:
a.
Tại $x=5$ thì $B=\frac{5+3}{5-2}=\frac{8}{3}$
b.
\(A=\frac{x^2-x+1}{(x-2)(x+2)}+\frac{2(x+2)}{(x-2)(x+2)}-\frac{x-2}{(x-2)(x+2)}=\frac{x^2-x+1+2(x+2)-(x-2)}{(x-2)(x+2)}\)
\(=\frac{x^2+7}{(x-2)(x+2)}\)
c.
\(P=A:B(x+2)=\frac{x^2+7}{(x-2)(x+2)}:\frac{x+3}{x-2}.(x+2)=\frac{x^2+7}{x+3}\)
Áp dụng BĐT Cô-si:
$x^2+1\geq 2|x|\geq 2x$
$\Rightarrow x^2+7\geq 2x+6=2(x+3)$
$\Rightarrow P\geq \frac{2(x+3)}{x+3}=2$
Vậy $P_{\min}=2$. Giá trị này đạt tại $x^2=1\Leftrightarrow x=\pm 1$ (tm)
LC
0
CH
giải giúp mình bài nay bằng máy tính casio hộ mình nha(nhớ giải chi tiết hộ mình)
tính: \(1023456^3\)
6
NM
1
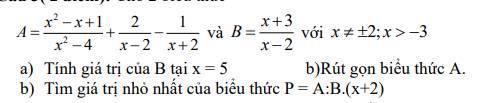
\(6-\sqrt{17}=\sqrt{36}-\sqrt{17}\)
Với :
\(\sqrt{36}-\sqrt{17}>\sqrt{31}-\sqrt{17}\)
Mặt khác :
\(\sqrt{31}-\sqrt{17}>\sqrt{31}-\sqrt{19}\)
Nên :
\(6-\sqrt{17}>\sqrt{31}-\sqrt{19}\)
Cách khác:
Ta có: \(\left(\sqrt{31}-\sqrt{19}\right)^2=50-2\sqrt{589}\)
\(\left(6-\sqrt{17}\right)^2=53-12\sqrt{17}=50+3-12\sqrt{17}\)
mà \(-2\sqrt{589}< 3-12\sqrt{17}\)
nên \(\sqrt{31}-\sqrt{19}>6-\sqrt{17}\)