K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
1
6 tháng 11 2015
Xét cả hai trường hợp sau:
a) Xét trường hợp điểm M nằm giữa hai điểm A và N; Điểm N nằm giữa hai điểm B và M.
- Vì M nằm giữa A và M nên AN= AM+MN (1)
- Vi N nằm giữa B và M nên BM= BN + MN (2)
Mà AN= BM (đề bài) nên từ (1) và (2) suy ra AM + MN = BN + MN
Do đó: AM = BN.
b) Xét trường hợp điểm N nằm giữa A và M; điẻm M nằm giữa B và N.
- Vì N nằm giữa A và M nên AN + NM= AM (3)
- Vì M nằm giữa B và N nên BM + MN= BN(4)
Mà AN=BM(Đề bài) nên từ (3) và(4) AM=BN
VT
1
VT
30 tháng 11 2015
Cho đoạn thẳng AB. Trên tia đối của tia AB lấy điểm M, trên tia đối của tia BA lấy điểm N sao cho AM = BN. So sánh BM và AN
T
12 tháng 10 2016
a) Xét điểm M nằm giữa hai điểm A và N.Điểm N nằm giữa hai điểm B và M.
-Vì M nằm giữa A và M nên AN= AM+MN(1).
-Vì N nằm giữa B và M nên BM= BN+MN(2),mà AN =BM nên (1) và (2) suy ra AM+MN= BN+MN.
Do đó:AM=BN.
b)Xét trường hợp điểm N nằm giữa A và M,điểm M nằm giữa B và N
-Vì N nằm giữa A nên AN+NM=AM(3).
-Vì M nằm giữa B nên BM+MN=BN(4),mà AM=BM nên từ (3) và (4) AM=BN
18 tháng 10 2017
Trường hợp 1: Vì M nằm giữa A và B ta có:
AM+MB=AB => AM=AB-MB=AB-AN ( vì AN =AB )
Vậy AM=BN
Trường hợp 2: Vì N nằm giữa A và B ta có:
AN+NB=AB =>NB=AB-AN
Vậy AM=BN
CM
5 tháng 1 2019
Chúng ta sẽ giải bài toán theo hai trường hợp như trong hình:
Trường hợp a)
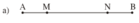
Vì M nằm giữa hai điểm A và N nên AN = AM + MN
Vì N nằm giữa hai điểm B và M nên BM = BN + MN
Theo đề bài: AN = BM nên AM + MN = BN + MN ⇒ AM = BN
(áp dụng tính chất: a + b = c + b ⇒ a = c)
Trường hợp b)
Vì N nằm giữa hai điểm A và M nên AN + MN = AM ⇒ AN = AM - MN
Vì M nằm giữa hai điểm B và N nên BM + MN = BN ⇒ BM = BN - MN
Theo đề bài: AN = BM nên AN - MN = BN - MN ⇒ AM = BN
(áp dụng tính chất: a - b = c - b ⇒ a = c)
Tóm lại: trong cả hai trường hợp thì hai đoạn thẳng AM và BN có độ dài bằng nhau
có 3 trường hợp xảy ra.
TH1: nếu \(a=b\Rightarrow a^n=b^n\)
TH2: nếu \(a>b\Rightarrow a^n>b^n\)
TH3: nếu \(a< b\Rightarrow a^n< b^n\)
k mk nha.
#ngố
Nếu a > b thì an > bn ( n khác 0 )
Nếu a < b thì an < bn ( n khác 0 )
Nếu a = b thì an = bn ( n khác 0 )