PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
17 tháng 3 2019
Đáp án B
TH1: 4 chữ số a, b, c , d khác nhau → có C 9 4 số
TH2: Trong 4 chữ số a, b, c , d có 3 chữ số giống nhau → có 3 C 9 3 số
TH3: Trong 4 chữ số a, b, c , d có 2 chữ số giống nhau → có 2 C 9 2 số
TH4: TH1: 4 chữ số a, b, c , d giống nhau → có C 9 1 số
Vậy có tất cả C 9 4 + 3 C 9 3 + 2 C 9 2 + C 9 1 = 459 số cần tìm
CM
10 tháng 8 2017
Đáp án B
Phương pháp:
Khi chọn bất kì bộ 3 số từ các số của tập số đã cho, ta luôn sắp xếp 3 số đó theo thứ tự từ bé đến lớn bằng duy nhất một cách.
Nếu trong 3 số đã chọn, tồn tại số 0 thì do a<b<c nên a = 0: Loại.
Vậy, số các số tự nhiên thỏa mãn yêu cầu đề bài bằng số cách chọn bất kì 3 số trong tập số {1;2;3;4;5;6}
Cách giải: Số các số tự nhiên thỏa mãn yêu cầu đề bài bằng số cách chọn bất kì 3 số trong tập số {1;2;3;4;5;6} và bằng C 20 3 = 20
7 tháng 3 2020
Theo đề bài ta thấy a,b,c≥1a,b,c≥1. Các số thỏa yc có các dạng sau:
1/ Dạng ¯¯¯¯¯¯¯1bc1bc¯:
¯¯¯¯¯¯¯¯11c11c¯ có 99 số
¯¯¯¯¯¯¯¯12c12c¯ có 88 số
.
.
.
¯¯¯¯¯¯¯¯19c19c¯ có 11 số
Vậy dạng này có C210=45C102=45 số
2/ Dạng ¯¯¯¯¯¯¯2bc2bc¯:
¯¯¯¯¯¯¯¯22c22c¯ có 88 số
¯¯¯¯¯¯¯¯23c23c¯ có 77 số
.
.
.
¯¯¯¯¯¯¯¯29c29c¯ có 11 số
Vậy dạng này có C29=36C92=36 số
Tương tự:
.
.
.
.
.8/ Dạng ¯¯¯¯¯¯¯8bc8bc¯:
¯¯¯¯¯¯¯¯88c88c¯ có 22 số
¯¯¯¯¯¯¯¯89c89c¯ có 11 số
Vậy dạng này có C23=3C32=3 số
9/ Dạng ¯¯¯¯¯¯¯9bc9bc¯:
¯¯¯¯¯¯¯¯99c99c¯ có 11 số
Vậy dạng này có C22=1C22=1 số
Do đó số các số thỏa yc đề bài là:
C210+C29+C28+C27+C26+C25+C24+C23+C22=165C102+C92+C82+C72+C62+C52+C42+C32+C22=165 số
CM
28 tháng 7 2018
Đáp án B.
Sắp xếp 4 số tự nhiên 1, 2, 3, 4 theo thứ tự khác nhau, ta sẽ được một số tự nhiên có 4 chữ số khác nhau. Vậy số cần lập là 4! = 24 (số).
CM
13 tháng 10 2018
Đáp án B
Sắp xếp 4 số tự nhiên 1, 2, 3, 4 theo thứ tự khác nhau ta sẽ được các số tự nhiên có 4 chữ số khác nhau => Có 4 ! = 24 số.
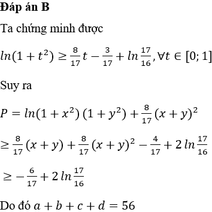
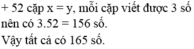
Đáp án A.
Ta có 3969000 = 2 3 . 3 4 . 5 3 . 7 2 . Suy ra các ước số của 3969000 có dạng 2 a . 3 b . 5 c . 7 d với a ∈ 0 ; 1 ; 2 ; 3 , b ∈ 0 ; 1 ; 2 ; 3 ; 4 , c ∈ 0 ; 1 ; 2 ; 3 , d ∈ 0 ; 1 ; 2 .
* Chọn a có 4 cách.
* Với mỗi cách chọn a có 5 cách chọn b.
* Với mỗi cách chọn a,b có 4 cách chọn c.
* Với mỗi cách chọn a,b,c có 3 cách chọn d.
Vậy số 3969000 có tất cả 4 . 5 . 4 . 3 = 240 ước số tự nhiên.