Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Chứng minh thuận:
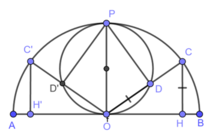
Từ O kẻ đường thẳng vuông góc với AB cắt nửa đường tròn đường kính AB tại P.
Vì O cố dịnh, đường tròn đường kính AB cố định nên P cố định.Nối PD
Ta có: OP // CH (cùng ⊥ AB)
Xét hai tam giác HCO và DOP ta có:
OD = CH (gt)
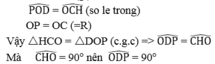
Khi C chuyển động trên nửa đường tròn đường kính AB thì D thay đổi tạo với hai đầu đọan thẳng OP cố định một góc 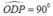
Vậy D chuyển động trên đường tròn đường kính OP
*Chứng minh đảo
Lấy điểm D’ bất kì trên đường tròn đường kính OP ,nối OD’ cắt nửa đường tròn đường kính AB tại C’.Nối PD’ và C’H’ ⊥ AB
Xét hai tam giác C’H’O và PD’O ta có:
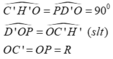
Vậy △ C’H’O = △ PD’O (c.g.c) ⇒ C’H’ = OD’
Quỹ tích điểm các điểm D khi C chuyển động trên nửa đường tròn đường kính AB là đường tròn đường kính OP, với 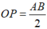

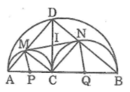
Gọi P là trung điểm của AC, Q là trung điểm của BC, I là giao điểm của MN với DC
Vì CMDN là hình chữ nhật nên IC = IM = ID = IN
Tam giác CNI cân tại I nên ![]() (3)
(3)
Tam giác CNQ cân tại Q nên ![]() (4)
(4)
Vì AB ⊥ CD nên ![]() =
90
°
(5)
=
90
°
(5)
Từ (3), (4) và (5) suy ra: ![]() =
90
°
hay MN ⊥ QN
=
90
°
hay MN ⊥ QN
Vậy MN là tiếp tuyến của đường tròn đường kính BC
Tam giác CMI cân tại I nên 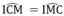 (6)
(6)
Tam giác CMP cân tại P nên 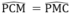 (7)
(7)
Vì AB ⊥ CD nên 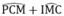 =
90
°
(8)
=
90
°
(8)
Từ (6), (7) và (8) suy ra: 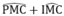 =
90
°
hay MN ⊥ PM
=
90
°
hay MN ⊥ PM
Vậy MN là tiếp tuyến của đường tròn đường kính AC

a: góc AMC=1/2*180=90 độ
=>góc DMC=90 độ
góc CNB=1/2*180=90 độ
=>góc DNC=90 độ
Kẻ tiếp tuyến Cx của hai đường tròn đường kính AC,CB, Cx cắt MN tại I
Xét (E) có
IC,IM là tiếp tuyến
=>IC=IM
Xét (F) có
IN,IC là tiếp tuyến
=>IN=IC=IM
Xét ΔMCN có
CI là trung tuyến
CI=MN/2
=>ΔMCN vuông tại C
góc DMC=góc DNC=góc MCN=90 độ
=>DMCN là hcn
b: ΔDCA vuông tại C có CM vừa là đường cao
nên DM*DA=DC^2
ΔDCB vuông tại C có CN là đường cao
nên DN*DB=DC^2=DM*DA

Gọi O, J lần lượt là trung điểm của AB và MB.
Do MB là đường kính của nửa đường tròn tâm J nên ^MIB=90o⇒^CIM=90o.
Vậy nên tứ giác CHMI nội tiếp.
⇒^HIM=^HCM.
Tam giác ACM cân tại C nên ^HCM=^HCA.
Mà ^HCA=^HBC (Cùng phụ góc CAB)
Tam giác IJB cân tại J nên ^HBC=^JIB.
Tóm lại : ^HIM=^JIB⇒^HIM+^MIJ=^JIB+^MIJ
⇒^HIJ=^MIB=90o.
Vậy nên HI là tiếp tuyến tại I của đường trong đường kính MB
Gọi O, J lần lượt là trung điểm của AB và MB.
Do MB là đường kính của nửa đường tròn tâm J nên .
Vậy nên tứ giác CHMI nội tiếp.
.
Tam giác ACM cân tại C nên .
Mà (Cùng phụ góc CAB)
Tam giác IJB cân tại J nên .
suy ra :
Vậy nên HI là tiếp tuyến tại I của đường trong đường kính MB.


* Kết luận :
Quỹ tích các điểm D khi C chạy trên nửa đường tròn đường kính AB là đường tròn đường kính OP, với \(OP=\dfrac{AB}{2}\)

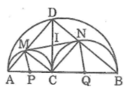
Tam giác ABD nội tiếp trong đường tròn có AB là đường kính nên ![]() = 90o hay
= 90o hay ![]() =
90
°
=
90
°
Tam giác ACM nội tiếp trong đường tròn có AC là đường kính nên ![]() =
90
°
=
90
°
Suy ra: CM ⊥ AD ⇒ ![]() =
90
°
=
90
°
Tam giác BCN nội tiếp trong đường tròn có AC là đường kính nên ![]() =
90
°
=
90
°
Suy ra: CN ⊥ BD ⇒  =
90
°
=
90
°
Tứ giác CMDN có ba góc vuông nên nó là hình chữ nhật
Chọn đáp án A
Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB