Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
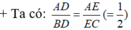
Nên theo định lí ta- let đảo ta có: DE // BC.
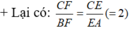
Nên theo định lí ta- let đảo ta có: EF // AB.
b) Tứ giác BDEF là hình bình hành vì có các cặp cạnh đối song song với nhau
c) Tứ giác BDEF là hình bình hành ⇒ DE = BF = 7
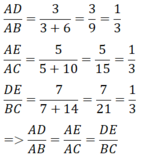
Ba cạnh của ΔADE tương ứng tỉ lệ với ba cạnh của ΔABC

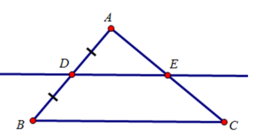
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

a) Đường thẳng \(d:y = 2x\) và \(d':y = x\) đều có dạng \(y = ax\) nên giao điểm của hai đường thẳng là \(O\left( {0;0} \right)\) (cả hai đường thẳng đều đi qua điểm \(O\left( {0;0} \right)\).
b)
- Hệ số góc của đường thẳng \(d:y = 2x\) là\(a = 2\).
- Hệ số góc của đường thẳng \(d':y = x\) là\(a = 1\).
Hai đường thẳng có hệ số góc khác nhau thì cắt nhau.
c) Vì \(d\) và \(d''\) cắt nhau nên chúng không thể song song với nhau hoặc trùng nhau. Do đó, hệ số góc của \(d\) và \(d''\) phải khác nhau. Khi đó, hệ số góc của \(d''\) khác 2.

a) +)Xét tg ABD có: CE //BD(gt)
Áp dụng đl Ta-let, ta có:
AB/AC=AD/AE
+) Xét tam giác ADC có: FE // CD(gt)
Áp dụng đl Ta-let,ta có:
AC/AF=AD/AE
b)Từ câu a), ta có:
AB/AC=AC/AF
->AC.AC=AB.AF
->AC^2=AB.AF

Áp dụng định lí 1 đường trung bình của tam giác
ΔADC có E là trung điểm AD và EI song song với cạnh DC
⇒ Điểm I là trung điểm AC
ΔABC có I là trung điểm AC và FI song song với cạnh AB
⇒ điểm F là trung điểm BC
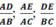 và cho nhận xét về mối liên hệ giữa các cặp cạnh tương ứng của hai tam giác ADE và ABC.
và cho nhận xét về mối liên hệ giữa các cặp cạnh tương ứng của hai tam giác ADE và ABC.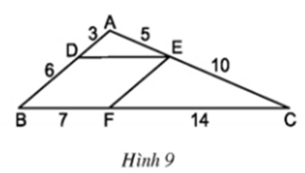

a) Đường thẳng \(d:y = 2x + 3\) có hệ số góc là \(a = 2\).
Đường thẳng \(d':y = 2x - 2\) có hệ số góc là \(a' = 2\).
Hệ số góc của hai đường thẳng \(d\) và \(d'\) bằng nhau.
Từ đồ thị ta thấy, hai đường thẳng \(d\) và \(d'\) song song với nhau.
b) Đường thẳng \(d''\) đi qua gốc tọa độ \(O\) nên có dạng \(y = a''x\).
Từ đồ thị ta thấy, \(d''\) đi qua điểm \(\left( {1;2} \right)\) nên ta có:
\(2 = 1.a'' \Rightarrow a'' = 2\).
Do đó, đường thẳng \(d''\) là \(y = 2x\).