Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

Bài 1:
A B C D M N P Q E F
a) Xét tam giác ABC có M là trung điểm của AB (gt) ,E là trung điểm của AC (gt)
\(\Rightarrow ME\)là đường trung bình tam giác ABC
\(\Rightarrow ME=\frac{1}{2}BC\left(tc\right)\left(1\right)\)
Xét tam giác ADC có E là trung điểm của AC (gt) ,P là trung điểm của DC (gt)
\(\Rightarrow PE\)là đường trung bình của tam giác ADC
\(\Rightarrow PE=\frac{1}{2}AD\left(tc\right)\left(2\right)\)
mà \(AD=BC\left(gt\right)\left(3\right)\)
Từ (1) , (2) và (3) \(\Rightarrow EM=PE\)
CMTT: \(PE=FP,FM=ME\)
\(\Rightarrow ME=EP=PF=FM\)
Xét tứ giác MEPF có:
\(ME=EP=PF=FM\left(cmt\right)\)
\(\Rightarrow MEPF\)là hình thoi ( dhnb)
b) Vì \(MEPF\)là hình thoi (cmt)
\(\Rightarrow FE\)giao với MP tại trung điểm mỗi đường (tc) (4)
Xét tam giác ADB có M là trung điểm của AB(gt) ,Q là trung điểm của AD (gt)
\(\Rightarrow MQ\)là đường trung bình của tam giác ADB
\(\Rightarrow MQ//DB,MQ=\frac{1}{2}DB\left(tc\right)\left(5\right)\)
Xét tam giác BDC có N là trung điểm của BC(gt) , P là trung điểm của DC(gt)
\(\Rightarrow NP\)là đường trung bình của tam giác BDC
\(\Rightarrow NP//DB,NP=\frac{1}{2}DB\left(tc\right)\left(6\right)\)
Từ (5) và (6) \(\Rightarrow MQ//PN,MQ=PN\)
Xét tứ giác MQPN có \(\Rightarrow MQ//PN,MQ=PN\)
\(\Rightarrow MQPN\)là hình bình hành (dhnb)
\(\Rightarrow MP\)giao QN tại trung điểm mỗi đường (tc) (7)
Từ (4) và (7) \(\Rightarrow MP,NQ,EF\)cắt nhau tại một điểm
c) Xét tam giác ABD có Q là trung điểm của AD (gt), F là trung điểm của BD(gt)
\(\Rightarrow QF\)là đường trung bình của tam giác ADB
\(\Rightarrow QF//AB\left(8\right)\)
CMTT: \(FN//CD\)và \(EN//AB\)
Mà Q,F,E,N thẳng hàng
\(\Rightarrow AB//CD\)
Vậy để Q,F,E,N thẳng hàng thì tứ giác ABCD phải thêm điều kiện \(AB//CD\)

a) Ta chứng minh A N = C M A N ∥ C M ⇒ A M C N là hình bình hành.
Vì O là giao điểm của AC và BD, ABCD là hình chữ nhật nên O là trung điểm AC
Do ANCM là hình bình hành có AC và MN là hai đường chéo
⇒ O là trung điểm MN
b. Ta có: EM//AC nên E M D ^ = A C D ^ (2 góc so le trong)
NF//AC nên B N F ^ = B A C ^ (2 góc so le trong)
Mà A C D ^ = B A C ^ (vì AB//DC, tính chất hình chữ nhật)
⇒ E M D ^ = B N F ^
Từ đó chứng minh được ∆ E D M = ∆ F B N ( g . c . g )
⇒ E M = F N
Lại có EM//FN (vì cùng song song với AC)
Nên tứ giác ENFM là hình bình hành
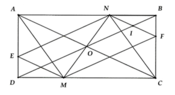
c) Tứ giác ANCM là hình thoi Û AC ^ MN tại O Þ M, N lần lượt là giao điểm của đường thẳng đi qua O, vuông góc AC và cắt CD, AB.
Khi đó M và N là trung điểm của CD và AB.
d) Ta chứng minh được DBOC cân tại O ⇒ O C B ^ = O B C ^ v à N F B ^ = O C F ^ (đv) Þ DBFI cân tại I Þ IB = IF (1)
Ta lại chứng minh được DNIB cân tại I Þ IN = IB (2)
Từ (1) và (2) Þ I là trung điểm của NF.