
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x+y=1 => (x+y)^3=1 <=> x^3+3x^2y+3xy^2+y^3=1
<=> x^3+y^3+3xy(x+y)=1
<=> x^3+y^3+3xy=1 Do x+y=1


2, kéo dài tia Am về phía M cắt DC tại F
Do ABCD là hình thang có góc A=góc D=90 độ nên AB song song CD
=> AB cũng song song DF => góc MCF = góc MBA ( so le trong )
xét tam giác MAB và tam giác MFC có:
góc CMF= góc AMB ( đối đỉnh)
MB=MC( M là trung điểm BC)
góc ABM= góc MCF( chứng minh trên)
=> tam giác MAB= tam giác MFC ( g.c.g)
=> MA=MF
Xét ta giác ADF có DM là đương trung tuyến ứng với cạnh huyền AF => DM=AM=MF
=> tam giác ADM và tam giác MDF cân tại M => góc MAD= góc MDA= 45 độ => góc MAB = 90 độ - góc MAD và góc MDC = 90 độ - góc MDA <=> góc MAB= 45 độ và góc MDC= 45 độ => góc MAB=góc MDC
3, Tương tự như câu 1
4, a+b+c=0 => a+b=-c => (a+b)^3=-c^3 <=> a^3+3a^2b+3ab^2+b^3=-c^3 => a^3+b^3+c^3=-3a^2b-3ab^2
<=> a^3+b^3+c^3= -3ab(a+b) Mà a+b=-c nên thay vào ta có:
a^3+b^3+c^3=-3ab(-c)=3abc mà abc=-2 => a^3+b^3+c^3=-6
a) cho x+y=1. Tính giá trị biểu thức x^3+ y^3+ 3xy
b) cho x-y=1. Tính giá trị biểu thức x^3- y^3- 3xy

x^3+ y^3+ 3xy
=(x+y)(x^2 -xy + y^2 ) + 3xy
=x^2 -xy + y^2 + 3xy
=x^2 + 2xy + y^2
=(x+y)^2 =1
=> x^3+ y^3+ 3xy=1

13 = (\(x+y\))3 = \(x^3\) + 3\(x^2\)y + 3\(xy^2\) + y3 = \(x^3\)+y3+3\(xy\)(\(x+y\))
1 = \(x^3\)+y3+3\(xy\)
13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\)y + 3\(xy\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)

b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)

Phan Văn Hiếu Bài của bạn ngay từ dòng đầu đã sai hướng làm rồi nhé :)
Ta có :
\(x^3+y^3+3xy\)
\(=\left(x^3+3x^2y+3xy^2+y^3\right)+3xy-3x^2y-3xy^2\)
\(=\left(x+y\right)^3-3xy\left(x+y-1\right)\)
Thay \(x+y=1;\) có :
\(=1^3-3xy\left(1-1\right)\)
\(=1-0\)
\(=1\)
Vậy ...
\(x^3+y^3+3xy=\left(x+y\right)\left(x^2+xy+y^2\right)+3xy\)
\(=x^2+2xy+y^2+2xy\)
\(=2xy\)
đế đây mk chịu

ta có : x3 + y3 + 3xy = (x+y)(x2 -xy +y2) +3xy =x2-xy+y2+3xy= (x+y)2=1
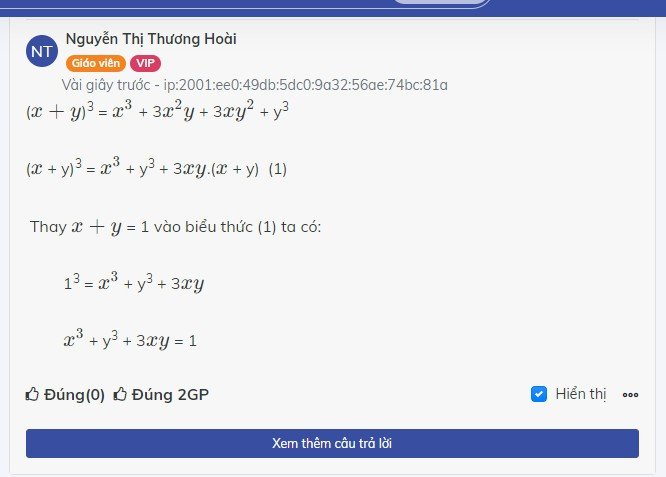
x3+y3+3xy
= (x+y) ( x2-xy+y2) + 3xy
= 1 .( x2-xy+y2)+ 3xy
= x2-xy+y2+3xy
= x2+2xy+y2
=( x+y )2
= 12
=1
lik e nha