Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c: =>3x^2+3y^2=39 và 3x^2-2y^2=-6
=>5y^2=45 và x^2=13-y^2
=>y^2=9 và x^2=4
=>\(\left\{{}\begin{matrix}x\in\left\{2;-2\right\}\\y\in\left\{3;-3\right\}\end{matrix}\right.\)
d: \(\Leftrightarrow\left\{{}\begin{matrix}5\sqrt{x}=5\\\sqrt{x}-\sqrt{y}=-\dfrac{11}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\\sqrt{y}=1+\dfrac{11}{2}=\dfrac{13}{2}\end{matrix}\right.\)
=>x=1 và y=169/4
b: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3x+3-3}{x+1}-\dfrac{2}{y+4}=4\\\dfrac{2x+2-2}{x+1}-\dfrac{5}{y+4}=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{3}{x+1}-\dfrac{2}{y+4}=4-3=1\\-\dfrac{2}{x+1}-\dfrac{5}{y+4}=9-2=7\end{matrix}\right.\)
=>x+1=11/9 và y+4=-11/19
=>x=2/9 và y=-87/19

Bài 1 :
a) Cái này cậu tự vẽ được nhé, cũng dễ mà :v tại tớ không biết vẽ trên đây :vvv
b)
*Xét A\(\left(3;\dfrac{9}{10}\right)\)
Thay x = 3 , y = \(\dfrac{9}{10}\) vào đồ thị hàm số , ta có
y = \(\dfrac{1}{10}x^2\)
\(\Rightarrow\dfrac{9}{10}=\dfrac{1}{10}\cdot3^2=\dfrac{9}{10}\)( Đúng )
Vậy điểm A thuộc đồ thị hàm số
*Xét B\(\left(-5;\dfrac{5}{2}\right)\)
Thay x = -5 , y = \(\dfrac{5}{2}\)vào đồ thị hàm số, ta có
\(y=\dfrac{1}{10}x^2\)
\(\Rightarrow\dfrac{5}{2}=\dfrac{1}{10}\cdot\left(-5\right)^2=\dfrac{25}{10}=\dfrac{5}{2}\) (Đúng)
Vậy điểm B thuộc đồ thị hàm số
* Xét \(C\left(-10;1\right)\)
Thay x=-10 ; y = 1 vào đồ thị hàm số, ta có
\(y=\dfrac{1}{10}x^2\)
\(\Leftrightarrow1=\dfrac{1}{10}\cdot\left(-10\right)^2=\dfrac{1}{10}\cdot100=10\) ( Vô lí )
Vậy điểm C không thuộc đồ thị hàm số
Bài 2:
* Xét A \(\left(\sqrt{2};m\right)\)
Thay x = \(\sqrt{2}\) vào đồ thị hàm số, có
y = \(\dfrac{1}{4}x^2=\dfrac{1}{4}\cdot\left(\sqrt{2}\right)^2=\dfrac{1}{4}\cdot2=\dfrac{1}{2}\)
Vậy \(A\left(\sqrt{2};\dfrac{1}{2}\right)\)
* Xét B( \(-\sqrt{2};m\))
Thay x = \(-\sqrt{2}\) vào ĐTHS, có
y= \(\dfrac{1}{4}\cdot\left(-\sqrt{2}\right)^2=\dfrac{1}{4}\cdot2=\dfrac{1}{2}\)
Vậy B\(\left(-\sqrt{2};\dfrac{1}{2}\right)\)
* Xét \(C\left(m;\dfrac{3}{4}\right)\)
Thay y= \(\dfrac{3}{4}\) vào ĐTHS, ta có
\(\dfrac{3}{4}=\dfrac{1}{4}\cdot x^2\)
=> \(x^2=\dfrac{3}{4}:\dfrac{1}{4}=3\)
\(\Rightarrow x=\pm\sqrt{3}\)
Vậy C \(\left(\sqrt{3};\dfrac{3}{4}\right)\) hoặc C\(\left(-\sqrt{3};\dfrac{3}{4}\right)\)

a) \(4xy\le\left(x+y\right)^2=1\)
=> \(xy\le4\)
Dấu "=" xảy ra <=> x = y = 1/2
b) A = \(A=x^2+2+\dfrac{1}{x^2}+y^2+2+\dfrac{1}{y^2}=\left(x^2+y^2\right)+\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)+4\ge2xy+\dfrac{2}{xy}+4=\left(32xy+\dfrac{2}{xy}\right)-30xy+4\ge8-\dfrac{30}{4}+4=\dfrac{9}{2}\)
Dấu "=" xảy ra <=> x = y = 1/2

Lời giải:
a)
Sử dụng pp biến đổi tương đương:
\(\frac{1}{a^2+1}+\frac{1}{b^2+1}\geq \frac{2}{ab+1}\Leftrightarrow \frac{a^2+b^2+2}{(a^2+1)(b^2+1)}\geq \frac{2}{ab+1}\)
\(\Leftrightarrow (ab+1)(a^2+b^2+2)\geq 2(a^2b^2+a^2+b^2+1)\)
\(\Leftrightarrow ab(a^2+b^2)+2ab\geq 2a^2b^2+a^2+b^2\)
\(\Leftrightarrow ab(a^2+b^2-2ab)-(a^2+b^2-2ab)\geq 0\)
\(\Leftrightarrow ab(a-b)^2-(a-b)^2\geq 0\)
\(\Leftrightarrow (ab-1)(a-b)^2\geq 0\) (luôn đúng với mọi $ab\geq 1$)
Ta có đpcm.
b) Áp dụng công thức của phần a ta có:
\(\frac{1}{a^4+1}+\frac{1}{b^4+1}\geq \frac{2}{1+(ab)^2}\)
Tiếp tục áp dụng công thức phần a: \(\frac{1}{1+(ab)^2}+\frac{1}{1+b^4}\geq \frac{2}{1+ab^3}\)
Do đó:
\(\frac{1}{a^4+1}+\frac{3}{b^4+1}\geq \frac{4}{1+ab^3}\)
Hoàn toàn tương tự: \(\frac{1}{b^4+1}+\frac{3}{c^4+1}\geq \frac{4}{1+bc^3}; \frac{1}{c^4+1}+\frac{3}{a^4+1}\geq \frac{4}{1+ca^3}\)
Cộng theo vế các BĐT trên thu được:
\(4\left(\frac{1}{a^4+1}+\frac{1}{b^4+1}+\frac{1}{c^4+1}\right)\geq 4\left(\frac{1}{1+ab^3}+\frac{1}{1+bc^3}+\frac{1}{1+ca^3}\right)\)
\(\Leftrightarrow \frac{1}{a^4+1}+\frac{1}{b^4+1}+\frac{1}{c^4+1}\geq \frac{1}{1+ab^3}+\frac{1}{1+bc^3}+\frac{1}{1+ca^3}\)
Ta có đpcm
Dấu bằng xảy ra khi $a=b=c=1$

a) \(a^2+b^2+c^2\ge ab+bc+ca\)
\(\Leftrightarrow2a^2+2b^2+2c^2\ge2ab+2bc+2ca\)
\(\Leftrightarrow a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
(Luôn đúng)
Vậy ta có đpcm.
Đẳng thức khi \(a=b=c\)
b) \(a^2+b^2+1\ge ab+a+b\)
\(\Leftrightarrow2a^2+2b^2+2\ge2ab+2a+2b\)
\(\Leftrightarrow a^2-2ab+b^2+b^2-2b+1+a^2-2a+1\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-1\right)^2+\left(a-1\right)^2\ge0\)
(Luôn đúng)
Vậy ta có đpcm
Đẳng thức khi \(a=b=1\)
Các bài tiếp theo tương tự :v
g) \(a^2\left(1+b^2\right)+b^2\left(1+c^2\right)+c^2\left(1+a^2\right)=a^2+a^2b^2+b^2+b^2c^2+c^2+c^2a^2\ge6\sqrt[6]{a^2.a^2b^2.b^2.b^2c^2.c^2.c^2a^2}=6abc\)
i) \(\dfrac{1}{a}+\dfrac{1}{b}\ge2\sqrt{\dfrac{1}{a}.\dfrac{1}{b}}=\dfrac{2}{\sqrt{ab}}\)
Tương tự: \(\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{2}{\sqrt{bc}};\dfrac{1}{c}+\dfrac{1}{a}\ge\dfrac{2}{\sqrt{ca}}\)
Cộng vế theo vế rồi rút gọn cho 2, ta được đpcm
j) Tương tự bài i), áp dụng Cauchy, cộng vế theo vế rồi rút gọn được đpcm
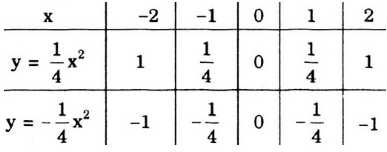
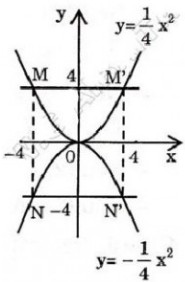



`D ( -1/4 = -1/4 xx 1^2) `
Chọn `C` và `D`
Vì `x=+-1` thì `y` đều có giá trị `= [-1]/4`