K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BH
27 tháng 2 2016
1. CMR với mọi số nguyên dương ta có:
A= x5/120 + x4/12 + 7x3/24 + 5x2/12 + x/5 luôn luôn dương
2. Cho a3 + 3ab2 =14 và b3 + 3a2b =13 . Tính: P= a2 _ b2
HV
27 tháng 2 2016
bui hai nam: s cóp lại y nguyên đề trong phần trả lời z bn =='
KY
15 tháng 9 2019
\(A=\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(\Leftrightarrow2A=\left(3-1\right)\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(\Leftrightarrow2A=\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(\Leftrightarrow2A=\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(\Leftrightarrow2A=\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(\Leftrightarrow2A=\left(3^{16}-1\right)\left(3^{16}+1\right)\)
\(\Leftrightarrow2A=3^{32}-1\)
\(\Leftrightarrow A=3^{31}-\frac{1}{2}\)
DH
0
BT
1
29 tháng 10 2022
b: =x^3+6x^2+9x^2+54x+20x+120
=(x+6)(x^2+9x+20)
=(x+6)(x+4)(x+5)
a: Đa thức này không phân tích được nha bạn
HN
1
21 tháng 8 2018
\(A=138^2+124.138+62^2\)
\(=138^2+2.62.138+62^2\)
\(=\left(138+62\right)^2\)
\(=200^2=40000\)
\(B=\left(100^2+98^2+...+2^2\right)-\left(99^2+97^2+....+3^2+1^2\right)\)
\(=100^2+98^2+....+2^2-99^2-97^2-....-3^2-1^2\)
\(=\left(100^2-99^2\right)+\left(98^2-97^2\right)+...+\left(4^2-3^2\right)+\left(2^2-1^2\right)\)
\(=\left(100+99\right)\left(100-99\right)+\left(98-97\right)\left(98+97\right)+...+\left(2-1\right)\left(2+1\right)\)
\(=199+195+191+....+7+3\)
\(=\frac{\left(199+3\right).\left[\left(199-3\right):4+1\right]}{2}=5050\)
Vậy B = 5050
DA
0
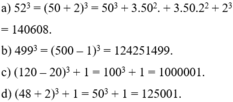
a) Ta có: \(120^3-60\cdot120^2+1200\cdot120-7999\)
\(=120^3-3\cdot120^2\cdot20+3\cdot120\cdot20^2-20^3+1\)
\(=\left(120-20\right)^3+1\)
\(=100^3+1\)
\(=1000001\)