
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, 2\(^3\) . x + 2005\(^0\) . x = 994-15:3+1\(^{2025}\)
8 .x + 1 . x = 990
x . [ 8 +1 ] = 990
x . 9 = 990
x = 990 : 9
x = 110

Vì : \(\left(2x-5\right)^{2022}\ge0\forall x,\left(3y+4\right)^{2024}\ge0\forall y\\ =>\left(2x-5\right)^{2022}+\left(3y+4\right)^{2024}\ge0\)
Do đó đề bài xảy ra khi và chỉ khi :
\(\left\{{}\begin{matrix}\left(2x-5\right)^{2022}=0\\\left(3y+4\right)^{2024}=0\end{matrix}\right.\\ =>\left(x;y\right)=\left(\dfrac{5}{2};-\dfrac{4}{3}\right)\)
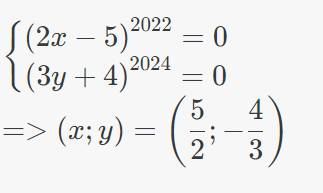 Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?
Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?

a, 2017-|x-2017| = x
=> |x - 2017| = 2017 - x
Th1: x \(\ge\)2017
=> x - 2017 = 2017 - x
=> x + x = 2017 + 2017
=> x = 2017 (thỏa mãn)
Th2: x < 2017
=> x - 2017 = -2017 + x
=> x - x = -2017 + 2017
=> 0 = 0
Vậy x = 2017
b, Vì \(\hept{\begin{cases}\left(2x-5\right)^{2018}\ge0\\\left(3y-7\right)^{2020}\ge0\\\left|x+y+z\right|\ge0\end{cases}\forall x,y,z}\)
\(\Rightarrow\left(2x-5\right)^{2018}+\left(3y-7\right)^{2020}+\left|x+y+z\right|\ge0\)
Mà \(\left(2x-5\right)^{2018}+\left(3y-7\right)^{2020}+\left|x+y+z\right|=0\)
Do đó \(\hept{\begin{cases}\left(2x-5\right)^{2018}=0\\\left(3y-7\right)^{2020}=0\\\left|x+y+z\right|=0\end{cases}\Leftrightarrow\hept{\begin{cases}2x-5=0\\3y-7=0\\x+y+z=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{5}{2}\\y=\frac{7}{3}\\z=\frac{-29}{6}\end{cases}}}\)

Ta có: \(\left(2x-1\right)^{2020}\ge0\forall x\)
\(\left(y-\frac{2}{5}\right)^{2020}\ge0\forall y\)
Do đó: \(\left(2x-1\right)^{2020}+\left(y-\frac{2}{5}\right)^{2020}\ge0\forall x,y\)
mà \(\left(2x-1\right)^{2020}+\left(y-\frac{2}{5}\right)^{2020}=0\)
nên \(\left\{{}\begin{matrix}\left(2x-1\right)^{2020}=0\\\left(y-\frac{2}{5}\right)^{2020}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-1=0\\y-\frac{2}{5}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=1\\y=\frac{2}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\frac{1}{2}\\y=\frac{2}{5}\end{matrix}\right.\)
Vậy: \(x=\frac{1}{2}\); \(y=\frac{2}{5}\)


Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn dễ hơn nhé.
Tìm x, y, z biết:\(\sqrt{\left(x-2024\right)^2}\) + ∣ x+ y -4z ∣ + \(\sqrt{5y^2}\) = 0 với x,y,z ϵ R

Lời giải:
Ta thấy: $\sqrt{(x-2024)^2}\geq 0$ với mọi $x\in\mathbb{R}$
$|x+y-4z|\geq 0$ với mọi $x,y,z\in\mathbb{R}$
$\sqrt{5y^2}\geq 0$ với mọi $y\in\mathbb{R}$
Do đó để tổng của chúng bằng $0$ thì bản thân mỗi số đó phải nhận giá trị $0$
Hay:
$\sqrt{(x-2024)^2}=|x+y-4z|=\sqrt{5y^2}=0$
$\Leftrightarrow x=2024; y=0; z=\frac{x+y}{4}=506$

helps me
^-^