K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 4 2016
Ta thấy
\(\frac{1}{5}<1\)
\(\frac{15}{2}<8\)
=> a thuộc các số nguyên từ 1 đến 8
Vậy a \(\in\) {1;2;3;4;5;6;7;8}
13 tháng 4 2016
ta có \(\frac{1}{5}\)=0,2
\(\frac{15}{2}\)=7,5
ta có 0,2<a<7,5
mà a là số nguyên nên a thuộc {1;2;3;4;5;6;7}
16 tháng 3 2016
(x-1)(x+5) / (x-1)(2x+6) = 1
=> (x-1)(x+5) = (x-1)(2x+6)
=> \(x^2+5x-x-5=2x^2+6x-2x-6\)
=> \(x^2-2x^2+4x-4x-5+6=0\)
=> \(-x^2+1=0\)
=> \(-x^2=-1\)
=> \(x^2=1\)
=> x thuộc {-1; 1}
16 tháng 3 2016
\(\frac{\left(x-1\right)\left(x+5\right)}{\left(x-1\right)\left(2x+6\right)}\)
đề vầy à
TT
16 tháng 1 2016
|-17-x|=7
=>-17-x=+7
TH1:
-17-x=7
x=-17-7
x=-24
TH2:
-17-x=-7
x=-17-(-7)
x=-10
Vậy :x=-24 hoặc -10
CM
13 tháng 9 2018
Chọn B
Cách giải: Ta có:
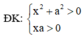
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
LT
2
22 tháng 3 2016
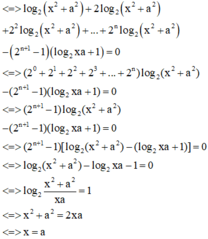
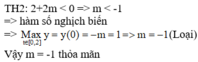
hello Ngọt
Ta có:
a x 0,56<4
Nếu a=8 thì 8 x 0,56=4,48>(loại)
Nếu a =7 thì 7x0,56=3,92<4(chọn)
Vì a là giá trị lớn nhất nên a=7
Chắc thế ngọt ak!Linh cũng ko chắc vì Linh chưa đc chấm mà!
CM
17 tháng 5 2018
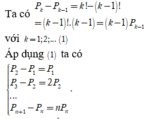
Cộng các đẳng thức ở (2) ta được 
Do
P
1
=
1
Theo đề, ta có 
Chọn A.
CH
0
27 tháng 1 2016
Ta có:
\(a.\left(a^2+3a+2\right)=6^{2005}+1\)
\(\Rightarrow a^3+3a^2+2a=6^{2005}+1\)
TH1: a là số lẻ
\(\Rightarrow a^3\) là số lẻ
\(3a^2\) là số lẻ
\(2a\) là số chẵn
\(\Rightarrow a^3+3a^2+2a\text{ ⋮ }2\)
Mà \(6^{2005}+1\) không chia hết cho 2
\(\Rightarrow\)Vô lý
TH2: a là số chẵn
\(\Rightarrow a^3\text{ ⋮}2\)
\(3a^2\text{ ⋮}2\)
Mà \(2a\text{ ⋮}2\)
\(\Rightarrow a^3+3a^2+2a\text{ ⋮}2\)
Mà \(6^{2005}+1\) không chia hết cho 2
Vậy không tồn tại a thỏa mãn điều kiện trên.
Nhiều số lắm bạn, ngồi liệt kê đau đầu luôn.
1/5=0,2;15/2=7/5
ta có 0,2<a<7,5
mà a là số nguyên suy ra a thuộc {1;2;3;4;5;6;7}