
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta thấy
\(\frac{1}{5}<1\)
\(\frac{15}{2}<8\)
=> a thuộc các số nguyên từ 1 đến 8
Vậy a \(\in\) {1;2;3;4;5;6;7;8}
ta có \(\frac{1}{5}\)=0,2
\(\frac{15}{2}\)=7,5
ta có 0,2<a<7,5
mà a là số nguyên nên a thuộc {1;2;3;4;5;6;7}

1/5=0,2;15/2=7/5
ta có 0,2<a<7,5
mà a là số nguyên suy ra a thuộc {1;2;3;4;5;6;7}

Đáp án A
Phương pháp: Sử dụng phương pháp tích phân từng phần tính F(x)
Cách giải:
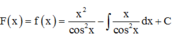
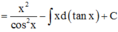
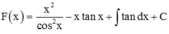
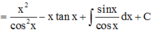

![]()
![]()
=> 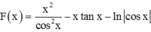
![]()
![]()
![]()
![]()
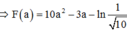
![]()
![]()

Ta có:
(abcd-c)-(abcd-b)=2017-2005=12
=>b-c=12
Vì b, c là các chữ số nên hiêu chúng lớn nhất chỉ là 9-0=9
Mà 12>9 => Vô lý
Như vậy không tồn tại b, c và cũng không tồn tại a,d
Vậy không có a, b, c, d thỏa mãn

ta có 4a+3b=a+3a+3b=a+(3a+3b)=a+[3*(a+b)]
ta có 3*(a+b) chia hết cho 5(vì a+b chia hết cho 5)
Mà a+b chia hết cho 5 nên a có thể chia hết cho 5 hoặc không chia hết cho5
Th1:a chia hết cho 5 thì a+[3*(a+b)]chia hết cho 5(vì 2 số cùng chia hết cho 5 thì tổng của chúng sẽ chia hết cho 5)
Th2:a không chia hết cho 5 thì a+[3*(a+b)]không chia hết cho 5(vì 2 số không chia hết cho 5 thì tổng của chúng sẽ không chia hết cho 5)
3a+b cũng tương tự như vậy thôi
3a+b=2a+a+b=2a+(a+b)
ta có (a+b) chia hết cho 5
Mà ƯCLN(2;5)=1 nên 2a có chia hết cho 5 hay không phụ thuộc vào a
ta cũng xét 2 trường hợp
Th1:a không chia hết cho 5 thì 3a+b không chia hết cho5
Th2:a chia hết cho 5 thì 3a+b chia hết cho 5
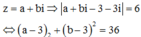
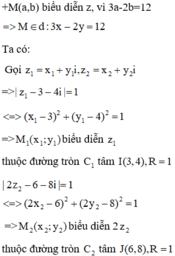

\(a.\left(a^2+3a+2\right)=6^{2005}+1\)
\(\Rightarrow a^3+3a^2+2a=6^{2005}+1\)
TH1: a là số lẻ
\(\Rightarrow a^3\) là số lẻ
\(3a^2\) là số lẻ
\(2a\) là số chẵn
\(\Rightarrow a^3+3a^2+2a\text{ ⋮ }2\)
Mà \(6^{2005}+1\) không chia hết cho 2
\(\Rightarrow\)Vô lý
TH2: a là số chẵn
\(\Rightarrow a^3\text{ ⋮}2\)
\(3a^2\text{ ⋮}2\)
Mà \(2a\text{ ⋮}2\)
\(\Rightarrow a^3+3a^2+2a\text{ ⋮}2\)
Mà \(6^{2005}+1\) không chia hết cho 2
Vậy không tồn tại a thỏa mãn điều kiện trên.