Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: 3=1.3=(-1).(-3)
TH1: x+1=1 => x=0 và xy-1=3 => 0y=4.( vô lí)=> loại
TH2: x+1=3 =>x=2 và xy-1=1 => xy=2 => 2y=2 => y=1
TH3: x+1= -1 => x=-2 và xy-1= -3 => xy= -2 => -2y=-2 => y=1
TH4: x+1= -3 => x=-4 và xy-1= -1 => xy=0 Suy ra -4y=0 Suy ra y=0.
Vậy (x,y) thuộc {(2;1); (-2;1) ; (-4;0)}
b) Vì lũy thừa cơ số 6 thì luôn luôn tận cùng là 6 vậy 6666= (...6). Tận cùng=6

a) ĐK: \(x\ge0,x\ne1,x\ne\frac{1}{4}\)
\(A=1+\left(\frac{2x+\sqrt{x}-1}{1-x}-\frac{2x\sqrt{x}-\sqrt{x}+x}{1-x\sqrt{x}}\right)\frac{x-\sqrt{x}}{2\sqrt{x}-1}\)
\(A=1+\left[\frac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(1-\sqrt{x}\right)}-\frac{\sqrt{x}\left(2\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(1-\sqrt{x}\right)\left(x+\sqrt{x}+1\right)}\right]\frac{\sqrt{x}\left(\sqrt{x}-1\right)}{2\sqrt{x}-1}\)
\(A=1+\left[\frac{2\sqrt{x}-1}{1-\sqrt{x}}-\frac{\sqrt{x}\left(2\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(1-\sqrt{x}\right)\left(x+\sqrt{x}+1\right)}\right]\frac{\sqrt{x}\left(\sqrt{x}-1\right)}{2\sqrt{x}-1}\)
\(A=1-\sqrt{x}+\frac{x\left(\sqrt{x}+1\right)}{x+\sqrt{x}+1}\)
\(A=\frac{x+1}{x+\sqrt{x}+1}\)
Để \(A=\frac{6-\sqrt{6}}{5}\Rightarrow\frac{x+1}{x+\sqrt{x}+1}=\frac{6-\sqrt{6}}{5}\)
\(\Rightarrow5x+5=\left(6-\sqrt{6}\right)x+\left(6-\sqrt{6}\right)\sqrt{x}+6-\sqrt{6}\)
\(\Rightarrow\left(1-\sqrt{6}\right)x+\left(6-\sqrt{6}\right)\sqrt{x}+1-\sqrt{6}=0\)
\(\Rightarrow x-\sqrt{6}.\sqrt{x}+1=0\)
\(\Rightarrow\orbr{\begin{cases}\sqrt{x}=\frac{\sqrt{2}+\sqrt{6}}{2}\\\sqrt{x}=\frac{-\sqrt{2}+\sqrt{6}}{2}\end{cases}}\Rightarrow\orbr{\begin{cases}x=2+\sqrt{3}\\x=2-\sqrt{3}\end{cases}}\left(tmđk\right)\)
b) Xét \(A-\frac{2}{3}=\frac{x+1}{x+\sqrt{x}+1}-\frac{2}{3}=\frac{3x+3-2x-2\sqrt{x}-2}{3\left(x+\sqrt{x}+1\right)}\)
\(=\frac{x-2\sqrt{x}+1}{3\left(x+\sqrt{x}+1\right)}=\frac{\left(\sqrt{x}-1\right)^2}{3\left(x+\sqrt{x}+1\right)}\)
Do \(x\ge0,x\ne1,x\ne\frac{1}{4}\Rightarrow\left(\sqrt{x}-1\right)^2>0\)
Lại có \(x+\sqrt{x}+1=\left(\sqrt{x}+\frac{1}{2}\right)+\frac{3}{4}>0\)
Nên \(A-\frac{2}{3}>0\Rightarrow A>\frac{2}{3}\).


|-17-x|=7
=>-17-x=+7
TH1:
-17-x=7
x=-17-7
x=-24
TH2:
-17-x=-7
x=-17-(-7)
x=-10
Vậy :x=-24 hoặc -10

Đáp án B
Gọi z = x + iy, x , y ∈ ℝ ta có:
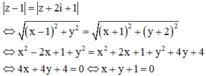
Vậy phương trình đường thẳng biểu diễn z là x + y + 1 = 0

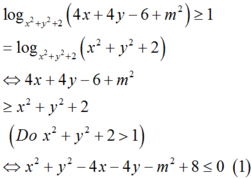
Ta có
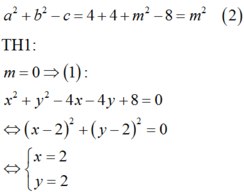
Cặp số x ; y = 2 ; 2 không thỏa mãn điều kiện .
![]()
Tập hợp các cặp số (x;y) thỏa mãn (1) là hình tròn C1(kể cả biên) tâm I1(2;2) bán kính R 1 = m .
Tập hợp các cặp số (x;y) thỏa mãn (2) là đường tròn C2 tâm I 2 - 1 ; 2 bán kính R 2 = 1 + 4 - 1 = 2 .
Để tồn tại duy nhất cặp số (x;y) thỏa mãn 2 điều kiện (1) và (2) Xảy ra 2 trường hợp sau:
TH1: C1; C2tiếp xúc ngoài
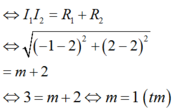
TH2: C1; C2 tiếp xúc trong và
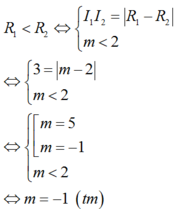
Vậy S = - 1 ; 1 .
Chọn D.

Chọn B
Cách giải: Ta có:
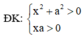
log 2 x 2 + a 2 + log 2 x 2 + a 2 + log 2 x 2 + a 2 + . . . + log . . . 2 ⏝ n c ă n x 2 + a 2 - 2 n + 1 - 1 log 2 x a + 1 = 0
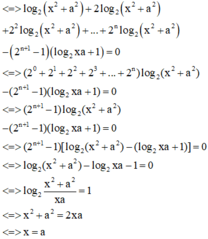
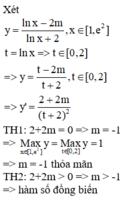
![]()

Điều kiện 1 3 ≤ x ≤ 10
Bất phương trình đã cho tương đương với:
log 2 3 x + 1 + 6 - 1 ≥ log 2 7 - 10 - x ⇔ 3 x + 1 + 6 2 ≥ 7 - 10 - x ⇔ 3 x + 1 + 2 10 - x ≥ 8 ⇔ 3 x + 1 + 4 3 x + 1 10 - x + 4 10 - x ≥ 64 ⇔ 4 3 x + 1 10 - x ≥ x + 23 ⇔ 16 3 x + 1 10 - x ≥ x + 23 2 ⇔ 49 x 2 - 418 x + 369 ≤ 0 ⇔ 1 ≤ x ≤ 369 49 ≈ 7 , 5
Mà x ∈ ℤ nên x ∈ 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7
Vậy có 7 giá trị nguyên của x
Đáp án D

Bài này chỉ có 1 đáp số thôi bạn, tại I-58I=58, nên -I-58I=-58
2x+(-12)=-I-58I
2x+(-12)=-58
2x = -58-(-12)
2x=-46 => x=-46:2=-23. Vậy x=-23
\(2x+\left(-12\right)=-\left|58\right|\)
\(2x-12=-58\)
\(2x=-58+12=-46\)
\(x=\frac{-46}{2}=-23\)
Vậy \(x=-23\)
(x-1)(x+5) / (x-1)(2x+6) = 1
=> (x-1)(x+5) = (x-1)(2x+6)
=> \(x^2+5x-x-5=2x^2+6x-2x-6\)
=> \(x^2-2x^2+4x-4x-5+6=0\)
=> \(-x^2+1=0\)
=> \(-x^2=-1\)
=> \(x^2=1\)
=> x thuộc {-1; 1}
\(\frac{\left(x-1\right)\left(x+5\right)}{\left(x-1\right)\left(2x+6\right)}\)
đề vầy à